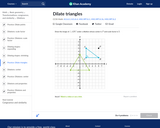
In this Khan Academy activity, students will plot the image of a triangle under a dilation and scale factor.
This video shows how we can use dilations to map a line into another, parallel, line.
This video defines center and using scale factor.
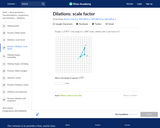
In this Khan Academy activity, students will plot the image of a quadrilaterals under a dilation and scale factor.
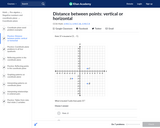
This practice provides seven problems about distance between points.
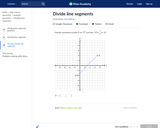
In this Khan Academy activity, students find the coordinates of a third point on a line given the coordinates of the other two.
This video shows how to divide two functions.
This video shows how to divide (x^2-3x+2) by (x-2) and then checks the solution.
This video shows students how to divide (2x^5-x^3+3x^2-2x+7) by (x-3) using synthetic division.
This video shows how the construction of the centroid by drawing medians divides the triangle into six smaller triangles of equal area.
In this Khan Academy activity, students will determine the domain and range of functions from their graph.
This Khan video finds the domain and range of f(x)=3x^2+6x-2.
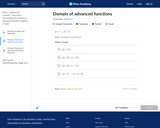
In this Khan Academy activity, students will practice finding the domain of advanced functions.
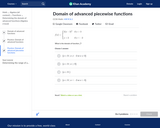
In this Khan Academy activity, students will practice finding the domain of advanced piecewise functions.
Students review gravitational potential energy, how to calculate it, and how to use it as a comparison to electric potential energy in these video lessons from Khan Academy.
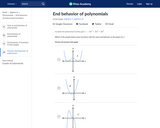
In this Khan Academy activity, students will determine what the end behavior of a polynomial looks like.
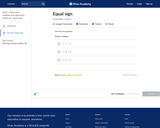
In this Khan Academy interactive, students will apply understanding of the equal sign to determine if equations involving addition and subtraction are true.
Khan video showing algebra application to the idea of midpoint.
This video solves the following equation by first simplifying the rational expression: x^2-(x^2-4)/(x-2)=4
This video solves (x^2-10x+21)/(3x-12)=(x-5)/(x-4), which has one real solution and one extraneous solution.