Subtracting a Negative
Opening
Subtracting a Negative
Discuss the following with your classmates.
In this lesson, you will model subtraction of integers as “taking away.” In Lesson 4, you will look at subtraction in a different way—as the distance between two points.
- Use the Hot Air Balloon interactive to model subtraction as taking away:
- Start at 0 and add heat to air (for a positive number) or weight (for a negative number) to move the balloon to the first number (the minuend).
- To subtract the second number (the subtrahend) from the first number, remove or take away units of heat or weights.
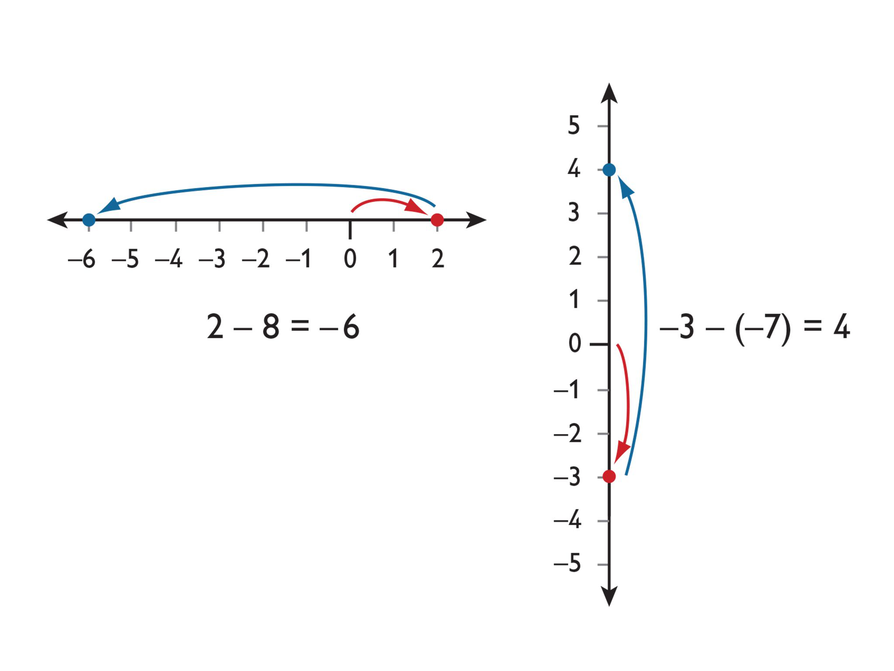
- For example, to model −3 − (−7):
- Start at 0 and add 3 units of weight to move the balloon to –3. To subtract –7, remove or take away 7 units of weight.
INTERACTIVE: Hot Air Balloon