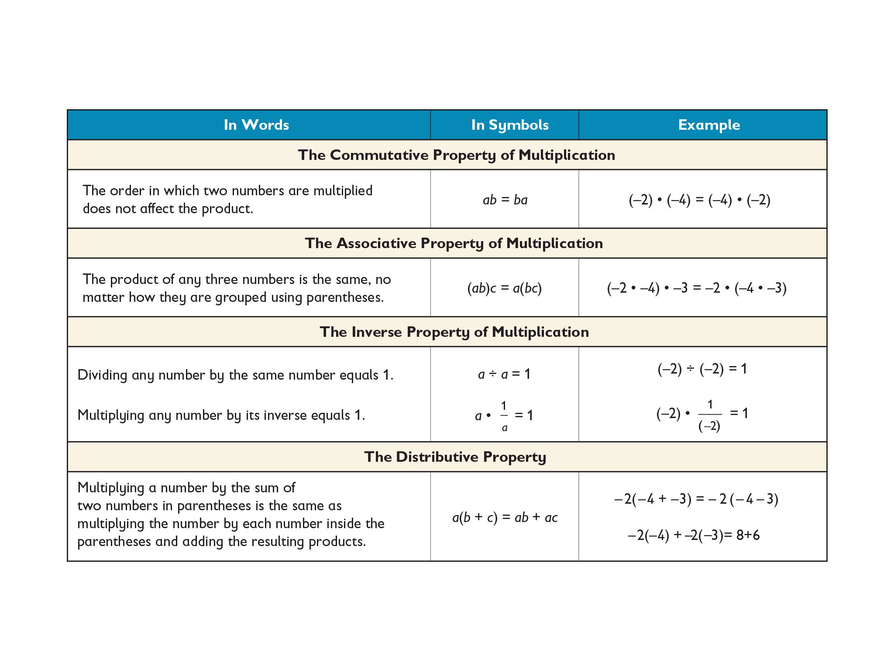
Review Properties of Operations
Opening
Review Properties of Operations
In the previous lesson, you built patterns to illustrate that the product of two negative numbers is a positive number. In today’s lesson, you will prove the product of two negative numbers is a positive number.
One way to prove the rule is through contradiction. Instead of trying to prove something is true, you prove that its opposite is false.
You want to prove that a negative times a negative equals a positive. The opposite is that a negative times a negative equals a negative.
So, if you can find something that contradicts the assumption that the product of two negative numbers is negative, then the product must instead be positive.
Discuss this proof with your class. Try to identify which property is used in each step:
- Assume that a negative times a negative equals a negative and find a contradiction.
| (−a) ⋅ (−b) | = | −c | Represent the assumption as an equation |
|---|---|---|---|
| (−1) ⋅ a ⋅ (−1) ⋅ b | = | (−1) ⋅ c | _ |
| (−1) ⋅ (−1) ⋅ a ⋅ b | = | (−1) ⋅ c | _ |
| (−1)(−1) ⋅ (−1)⋅ a ⋅ b | = | (−1)(−1) ⋅ c | _ |
| 1 ⋅ (−1) ⋅ a ⋅ b | = | 1 ⋅ c | _ |
| (−1) ⋅ a ⋅ b | = | c | _ |
| (−1) ⋅ (ab) | = | c | _ |
| −(ab) | = | c | _ |
- Since a and b are positive, so is ab. However, since c is also positive, the last step says that the opposite of a positive number is also positive, which is a contradiction!
- Since assuming that a negative times a negative leads to a contradiction, it must be false, and the opposite must be true. Therefore, a negative times a negative equals a positive.