The purpose of this task is to provide students with a concrete situation they can model by dividing a whole number by a unit fraction.
This task requries students to think about division by fractons.
The purpose of this task is for students to compare a number and its product with other numbers that are greater than and less than one.
The purpose of this task is to have students think about the meaning of multiplying a number by a fraction, and to use this understanding of fraction multiplication to make sense of the commutative property of multiplication in the case of fractions.
One common mistake students make when dividing fractions using visuals is the confusion between remainder and the fractional part of a mixed number answer.
The purpose of this task is to help students explore the meaning of fraction division and to connect it to what they know about whole-number division.
REMIX - Added accessibility enhancements.Students explore methods of dividing a fraction by a unit fraction.Key ConceptsIn this lesson and in Lesson 5, students explore dividing a fraction by a fraction.In this lesson, we focus on the case in which the divisor is a unit fraction. Understanding this case makes it easier to see why we can divide by a fraction by multiplying by its reciprocal. For example, finding 34÷15 means finding the number of fifths in 34. In this lesson, students will see that this is 34 × 5
This task requires students to recognize both "number of groups unknown" and "group size unknown" division problems in the context of a whole number divided by a unit fraction.
This task builds on a fifth grade fraction multiplication task and uses the identical context, but asks the corresponding ŇNumber of Groups UnknownÓ division problem.
This task builds on a fifth grade fraction multiplication task and uses the identical context, but asks the corresponding ŇNumber of Groups UnknownÓ division problem.
This task requires students to think about and compare fractions.
This task requires students to think about and compare fractions.
These two fraction division tasks use the same context and ask ŇHow much in one group?Ó but require students to divide the fractions in the opposite order. Students struggle to understand which order one should divide in a fraction division context, and these two tasks give them an opportunity to think carefully about the meaning of fraction division.
The purpose of this task is to help students see the connection between aÖb and ab in a particular concrete example. The relationship between the division problem 3Ö8 and the fraction 3/8 is actually very subtle.
These problems are meant to be a progression which require more sophisticated understandings of the meaning of fractions as students progress through them.
This task provides a context for performing division of a whole number by a unit fraction. This problem is a "How many groups?'' example of division.
This is the first of two fraction division tasks that use similar contexts to highlight the difference between the ŇNumber of Groups UnknownÓ a.k.a. ŇHow many groups?Ó (Variation 1) and ŇGroup Size UnknownÓ a.k.a. ŇHow many in each group?Ó (Variation 2) division problems.
This is the second of two fraction division tasks that use similar contexts to highlight the difference between the ŇNumber of Groups UnknownÓ a.k.a. ŇHow many groups?Ó (Variation 1) and ŇGroup Size UnknownÓ a.k.a. ŇHow many in each group?Ó (Variation 2) division problems.
Fractions and Decimals
Type of Unit: Concept
Prior Knowledge
Students should be able to:
Multiply and divide whole numbers and decimals.
Multiply a fraction by a whole number.
Multiply a fraction by another fraction.
Write fractions in equivalent forms, including converting between improper fractions and mixed numbers.
Understand the meaning and structure of decimal numbers.
Lesson Flow
This unit extends students’ learning from Grade 5 about operations with fractions and decimals.
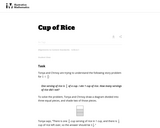
The first lesson informally introduces the idea of dividing a fraction by a fraction. Students are challenged to figure out how many times a 14-cup measuring cup must be filled to measure the ingredients in a recipe. Students use a variety of methods, including adding 14 repeatedly until the sum is the desired amount, and drawing a model. In Lesson 2, students focus on dividing a fraction by a whole number. They make a model of the fraction—an area model, bar model, number line, or some other model—and then divide the model into whole numbers of groups. Students also work without a model by looking at the inverse relationship between division and multiplication. Students explore methods for dividing a whole number by a fraction in Lesson 3, for dividing a fraction by a unit fraction in Lesson 4, and for dividing a fraction by another fraction in Lesson 6. Students examine several methods and models for solving such problems, and use models to solve similar problems.
Students apply their learning to real-world contexts in Lesson 6 as they solve word problems that require dividing and multiplying mixed numbers. Lesson 7 is a Gallery lesson in which students choose from a number of problems that reinforce their learning from the previous lessons.
Students review the standard long-division algorithm for dividing whole numbers in Lesson 8. They discuss the different ways that an answer to a whole number division problem can be expressed (as a whole number plus a remainder, as a mixed number, or as a decimal). Students then solve a series of real-world problems that require the same whole number division operation, but have different answers because of how the remainder is interpreted.
Students focus on decimal operations in Lessons 9 and 10. In Lesson 9, they review addition, subtraction, multiplication, and division with decimals. They solve decimal problems using mental math, and then work on a card sort activity in which they must match problems with diagram and solution cards. In Lesson 10, students review the algorithms for the four basic decimal operations, and use estimation or other methods to place the decimal points in products and quotients. They solve multistep word problems involving decimal operations.
In Lesson 11, students explore whether multiplication always results in a greater number and whether division always results in a smaller number. They work on a Self Check problem in which they apply what they have learned to a real-world problem. Students consolidate their learning in Lesson 12 by critiquing and improving their work on the Self Check problem from the previous lesson. The unit ends with a second set of Gallery problems that students complete over two lessons.