- Author:
- ERIN WOLFHOPE
- Subject:
- Mathematics
- Material Type:
- Lesson, Textbook
- Level:
- Upper Primary
- Tags:
- License:
- Creative Commons Attribution Share Alike
- Language:
- English
Education Standards
Adding and Subtracting Fractions Practice
Adding and Subtracting Fractions
Overview
This workbook was created through the efforts of three instructors at Scottsdale Community College in Scottsdale, Arizona. Any individual may download and utilize a digital copy of this workbook for free.
Introduction
In this lesson, we will concentrate on combining fractions through addition and subtraction (and save multiplication and division for the NEXT lesson!). When combining fractions through addition or subtraction, the idea of “unit fractions” and “copies of unit fractions” takes center stage. Look for this phrasing as you work through the MiniLesson.
The table below shows the specific whole-number related objectives that are the achievement goal for this lesson. Read through them carefully now to gain initial exposure to the terms and concept names for the lesson. Refer back to the list at the end of the lesson to see if you can perform each objective.
Add and subtract fractions with like denominators.
Add and subtract fractions with unlike denominators.
Add and subtract mixed numbers.
Explain the difference between CD, LCM, & LCD
Solve applications using fraction addition and subtraction.
Use correct order of operations when adding/subtracting fractions
The key terms listed below will help you keep track of important mathematical words and phrases that are part of this lesson. Look for these words and circle or highlight them along with their definition or explanation as you work through the MiniLesson.
Fraction
Unit Fraction
Common Denominator
Least Common Denominator (LCD)
Least Common Multiple (LCM)
Mathematical operations
PEMDAS
Adding and Subtracting Fractions with Like Denominators
Adding and Subtracting Fractions with Like Denominators
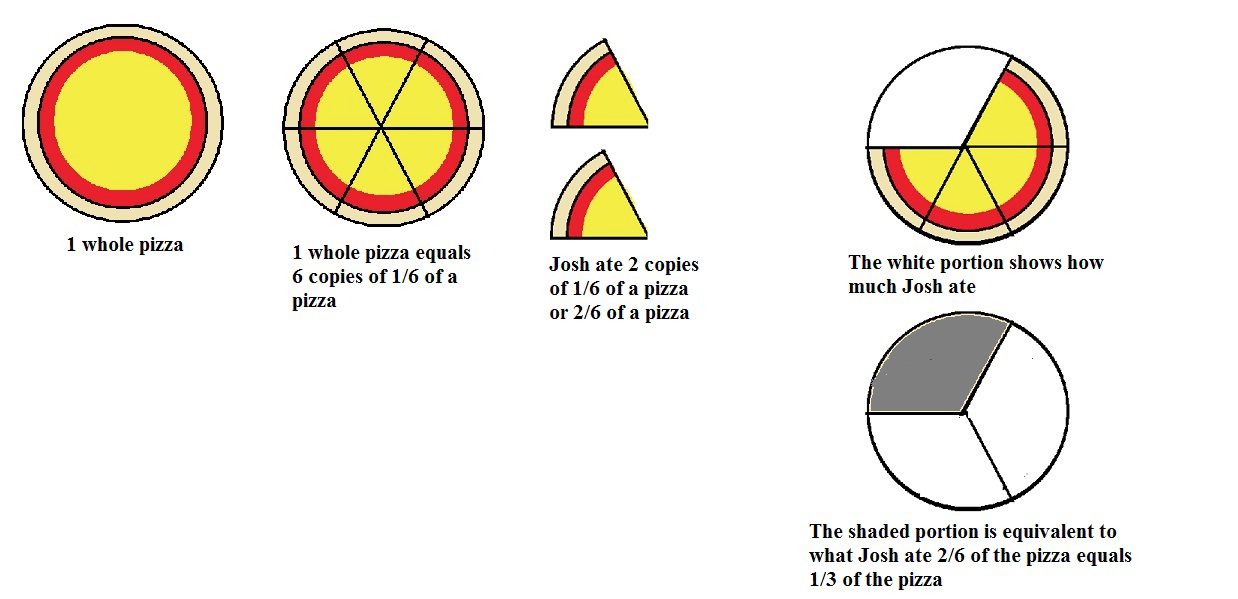
Suppose Josh ordered a pizza and sat down to watch football. The pizza was cut into 6 equal slices. During the first half of the game, he ate one slice and during the second half, he ate another. How much of the pizza did Josh eat?
2 slices out of 6 or \(\frac{2}{6} =\frac{1}{3}\)of the pizza (Remember to fully reduce!)
We can also look at it another way. Since the pizza was divided into 6 pieces, the “units” of the pizza division were sixths. The fraction\(\frac{1}{6}\) is a unit fraction. How many copies of the \(\frac{1}{6}\) size pieces did he eat? He ate 2 separate \(\frac:{1}{6}\) size pieces so he ate:
\(\frac{1}{6} + \frac{1}{6} = \frac{2}{6} =\frac{1}{3}\)of the pizza
Let’s see how the example above helps us with the problems below.
Example 1: Add. Write your answer in simplest form.
a. \(\frac{5}{12} +\frac{2}{12} =\)
b. \(\frac{3}{8} +\frac{7}{8} = \)
Example 2: Subtract. Write your answer in simplest form.
a. \(\frac{5}{8} - \frac{1}{8} =\)
b. \(\frac{11}{12} - \frac{7}{12} =\)
You Try
Example 3. Perform the indicated operations. Write your answer in simplest form.
a. \(\frac{4}{9} + \frac{2}{9} =\)
b. \(\frac{12}{13} - \frac{6}{13} =\)
Adding and Subtracting Fractions with Like Unlike Denominators
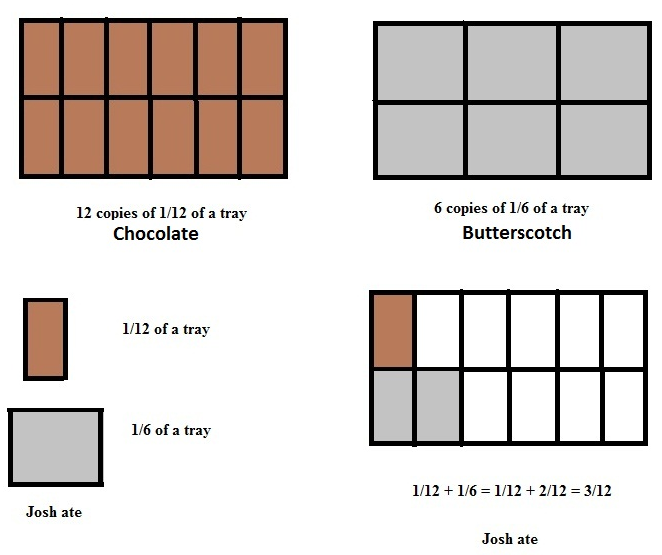
Let’s look at another situation. Suppose Josh had two trays of brownies to serve for desert at an upcoming party. One tray had chocolate brownies and the other had butterscotch.
The chocolate tray was cut into 12 equal pieces and the butterscotch tray into 6 equal pieces (big brownies!). Josh ate one brownie from each tray before his guests arrived. What fraction of the brownies on each tray did Josh eat? Josh ate:
\(\frac{1}{12}\) of the chocolate brownie tray | \(\frac{1}{6}\) of the butterscotch brownie tray |
What fraction of the brownies on a single tray did Josh eat? Josh ate:
\(\frac{1}{12} + \frac{1}{6}\) of the brownies on a single tray.
Hmmm.... how do we combine those? Did Josh eat \(\frac{2}{18} = \frac{1}{9}\)of the brownies? No, that does not makes sense. What if we divide the butterscotch tray into 12 pieces just like the chocolate tray? Josh originally had \(\frac{1}{6}\)of the butterscotch tray, which would be the same as \(\frac{2}{12} \)of the tray. Now can we combine the amounts?
\(\frac{1}{12} + \frac{2}{12} = \frac{3}{12}\)
Yes! Now that makes more sense. Josh ate \(\frac{1}{12}\) of the browniew on one tray and \(\frac{2}{12}\) of the brownies on the other dray for a total of \(\frac{3}{12} \) of the brownies on a single tray.
What we learned from the brownie example on the previous page is that to add two fractions they must have the same (common) denominator. Let’s see how this works with some additional examples.
Example 4: Add. Start by identifying a common denominator (CD). Write your answer as both an improper fraction and a mixed number if possible.
a. \(\frac{1}{2} + \frac{2}{3} =\)
b. \(\frac{3}{8} + \frac{5}{6} =\)
Example 5: Subtract. Start by identifying a common denominator (CD). Write your answer as both an improper fraction and a mixed number if possible.
a. \(\frac{2}{3} - \frac{1}{2} =\)
b. \(\frac{3}{4} - \frac{2}{5} =\)
You Try
Example 6: Perform the indicated operations Start by identifying a common denominator (CD). Write you answer as both and improper fraction and a mixed number if possible.
a. \(\frac{4}{5} + \frac{3}{8} =\)
b. \(\frac{4}{5} - \frac{11}{15} =\)
Rules for adding or subtracting fractions.
1. To add or subtract fractions with LIKE denominators, add or subtract the numerators as indicated and place over the like denominator. Reduce if possible.
2. To add or subtract fractions with UNLIKE denominators, obtain a common denominator then follow step 1 above. Be sure to reduce if possible.
Let’s see how these rules work when we start using mixed numbers.
Adding and Subtracting Mixed Numbers
Example 7: Perform the indicated operation. Start by identifying a common denominator (CD). Write your answer as both an improper fraction and a mixed number if possible.
a. \(1\frac{1}{5} + 2\frac{2}{3}=\)
b. \(4\frac{3}{5} - 1\frac{5}{6} = \)
You Try
Example 8: Perform the indicated operation. Start by identifiying a common denominator (CD). Write your answer as both an improper fraction and a mixed number if possible.
a. \(4\frac{1}{3} - 1\frac{3}{4} =\)
b. \(6\frac{1}{2} + 3\frac{5}{8} = \)
LCM vs LCD vs CD
Worked Example 9: Let’s distinguish between three vocabulary terms related to fractions.
LCD = Least Common Denominator
LCM = Least Common Multiple
CD = Common Denominator
Problem: Add \(\frac{1}{2} + \frac{1}{8}\) | To start this problem, what we need is a Common Denominator (CD) of the denominators 2 and 8. What number works? Well, we need a number that is divisible by both 2 and 8. Let’s try 2 times 8, which is 16. That works and guides the solution below: |
Step 1: \(\frac{1}{2} + \frac{1}{8}\) Step 2: \(=\frac{1*8}{2*8} + \frac{1*2}{8*2}\) Step 3: \(=\frac{8}{16} + \frac{2}{16}\) Step 4: \(=\frac{10}{16} = \frac{5}{8}\) | Step 1: Original problem |
However, notice that we had to reduce at the end. Let’s try another track. Let’s first find the LCM or Least Common Multiple of the denominators 2 and 8. Remember how that was done previously? List multiples of 2 and 8 to find the first one in common:
2: 2, 4, 6, 8, 10, 12, 14, 16... and 8: 8, 16, 24, 32,....
We can see that 8 is the LCM of 2 and 8. It is the smallest number that both 2 and 8 divide into evenly. Thus, it also fits the definition of the LCD or Least Common Denominator. LCD and LCM are really equal in a sense. Let’s see what happens when we use the LCD:
Step 1: \(\frac{1}{2} + \frac{1}{8}\) Step 2: \(=\frac{1*4}{2*4} + \frac{1}{8}\) Step 3: \(=\frac{4}{8} +\frac{1}{8} =\frac{5}{8}\) | We get the same result as above AND in fewer steps with no reducing required at the end. So, the motto is, use the LCD whenever possible and remember that the LCD and the LCM are the same number. |
Special Cases/Confusing Situations
Each of the examples below displays a little “oddity” or unusual situation that you may not be sure how to deal with the first time you see it. Refer back to these examples as needed while completing the HW or Practice problems.
Example 10: What if your numerator ends up being 0?
\(\frac{3}{5} - \frac{9}{15}\)
Example 11: What if your numerator ends up the same as your denominator?
\(\frac{1}{4} + \frac{6}{8}\)
Example 12: What if your numerator is a multiple of your denominator?
\(2\frac{1}{3} + 3\frac{4}{6}\)
You Try
Example 13: Perform the indicated operation. Write your answer in simplest form.
a. \(4\frac{2}{3} - 3\frac{4}{6}\)
b. \(4\frac{1}{3} + 2\frac{2}{3}\)
Applications of Fraction Addition
Example 14: In a bag of 100 M & M’s, 30 are brown, 20 are yellow, 20 are red, 10 are green, 10 are orange, and 10 are blue. What fraction of the M & M’s are brown, or blue?
GIVEN:
GOAL:
MATH WORK:
CHECK:
FINAL RESULT AS A COMPLETE SENTENCE:
You Try
Example 15: On a recent trip, Robert flew \(4\frac{2}{3}\) hours on his first flight and \(12\frac{1}{2}\) hours on his second flight. How many hours was he in the air? Leave your final answer as a mixed number.
GIVEN:
GOAL:
MATH WORK:
CHECK:
FINAL RESULT AS A COMPLETE SENTENCE:
Order of Operations with Fractions
Remember our order of operations from Lesson 1? We will use the same order when working with fraction expressions that involve multiple operations.
P Simplify items inside Parenthesis ( ), brackets [ ] or other grouping symbols first.
E Simplify items that are raised to powers (Exponents) M Perform Multiplication and Division next
D (as they appear from Left to Right)
A Perform Addition and Subtraction on what is left.
S (as they appear from Left to Right)
Example 16: Use order of operations to simplify the expression showing all possible steps.
a. \(\frac{5}{8} + \frac{3}{4} - \frac{4}{5} =\)
b. \((3 - \frac{1}{4}) - (\frac{1}{3} + \frac{1}{15}) =\)
You Try
Example 17:
Perform the indicated operations. Write your answer in simplest form. If applicable, write your answer as both an improper fraction and a mixed number.