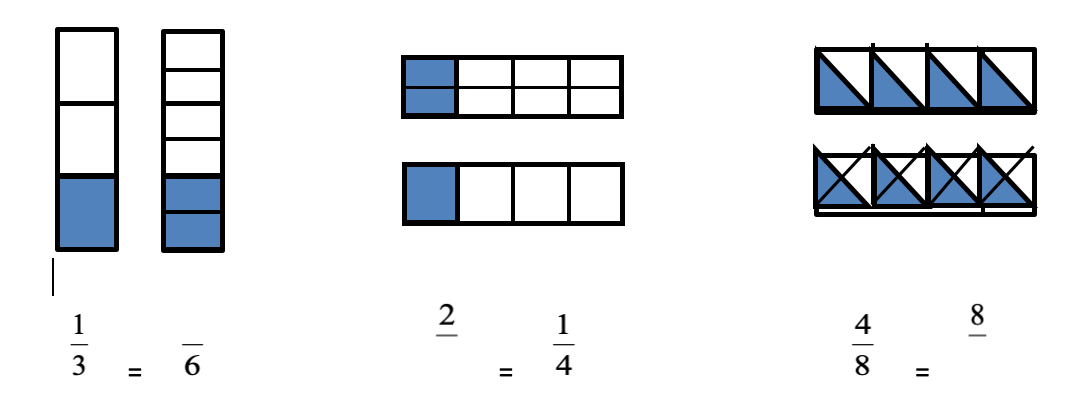Equivalent Fractions

Overview
Generate simple equivalent fractions by using visual fraction models and the number line.
This lesson is adapted from a lesson created by Engage NY: https://www.engageny.org/resource/grade-3-mathematics-module-5-topic-e-lesson-22/file/35446
The lesson image is Quarters by luca fruzza from the Noun Project.
Introduction
Introduce Equivalent Fractions using the Number Rock Video: https://numberock.com/lessons/equivalent-fractions/
Counting by Fractions Equal to Whole Numbers on the Number Line
Materials: (S) Personal white board
Note: This activity reviews the concept of naming equivalent fractions on the number line.
T: (Project a number line partitioned into 12 thirds.) Count by thirds. (Write fractions as students count.)
Ask students to write the fractions equal to whole numbers in order from least to greatest.
Practice
Mr. Ramos wants to put a wire on the wall. He puts 9 nails equally spaced along the wire. Draw a number line representing the wire. Label it from 0 at the first nail of the wire to 1 at the last nail. Mark each fraction where Mr. Ramos puts each nail.
- Build a number bond with unit fractions to 1 whole.
- Write the fraction of the nail that is equivalent to \(\frac{1}{2}\) of the wire.
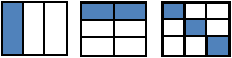
Let’s look at a model. These 3 wholes are the same. Name the shaded fraction as I point to the model.
Are these fractions equivalent? Work with your partner to use the number line to prove your answer. Be ready to share your thinking.
We Do
Write the missing parts of the fractions:
Why does it take 2 copies of \(\frac{1}{8}\) to show the same amount as 1 copy of \(\frac{1}{4}\) ? Explain your answer in words and pictures.
How many sixths does it take to make the same amount as \(\frac{1}{3}\) ? Explain your answer in words and pictures.
Why does it take 10 copies of 1 sixth to make the same amount as 5 copies of 1 third? Explain your answer in words and pictures.