- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Downloadable docs, Text/HTML
Drawing Figures on the Coordinate Plane

Overview
Students draw a figure on the coordinate plane that matches a written description.
Key Concepts
- Ordered pairs name locations on the coordinate plane. The first coordinate tells how many units to go left or right of the origin (0,0) along the x-axis. The second coordinate tells how many units to go up or down from the origin along the y-axis.
Goals and Learning Objectives
- Draw a figure that matches a description of a figure on the coordinate plane.
- Give coordinates of points on the coordinate plane.
- Write descriptions of figures on the coordinate plane.
Draw a Line on the Coordinate Plane
Lesson Guide
Review the convention for naming points on the coordinate plane.
Give students a minute to think about the problem. Then have them discuss the problem with a partner.
Discuss students’ solutions to the problem. For each proposed solution, have the class work together to prove or disprove that the line matches the description. Elicit that there is only one line segment that meets this description, the line segment where the other endpoint is (2.5,3).
Opening
Draw a Line on the Coordinate Plane
- On the Coordinate Plane Plotter, draw a line segment that meets the following description:
- One endpoint of the line segment is (−2.5,3).
- The point (0,3) is on the line segment.
- The line segment is 5 units long.
- Name the other endpoint.
INTERACTIVE: Coordinate Plane Plotter
Math Mission
Lesson Guide
Discuss the Math Mission. Students will draw a figure on the coordinate plane that matches a description.
Opening
Draw a figure on the coordinate plane that matches a description.
Draw a Figure
Lesson Guide
Have students work independently on each problem and then discuss their answers with a partner.
ELL: When ELLs work with a partner, allow them to use their language of origin if they are paired with a student who speaks that language.
SWD: Struggling math students may need explicit explanation of the connections between this new concept and previously learned concepts. Ask scaffolding questions to promote student “discovery” of these connections.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What do you know?
- What do you know about the lengths of the sides of a square?
- How long is a side of the square?
Student presents his work poorly.
- Have you checked your work?
- Is your work clear?
- Would someone be able to recognize your figure and its location on the coordinate plane?
Student has an incorrect solution.
- Have you checked your figure against its description?
- Where is the lower left corner of the square?
- How long is a side of your square?
- Does your square have sides that are all the same length?
Student has a correct solution.
- Explain your strategy for solving the problem.
Mathematical Practices
Mathematical Practice 6: Attend to precision.
Students will need to follow the description exactly in order to draw the correct figure. Identify examples of students who attend to precision and those who do not.
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who reason that a square has four sides of equal lengths, so each side must be 6 units long.
Answers
Work Time
Draw a Figure
Draw a figure that meets the following description and name the vertices.
- The figure is a square.
- The lower left corner is located at (−3.5,−4.5).
- The length of a side is 6 units.
INTERACTIVE: Coordinate Plane Plotter
Think about the characteristics of a square.
Name the Figure
Lesson Guide
Students describe a rectangle in the coordinate plane. If students are having trouble, you can suggest they read the hint.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Listen as partners share their answers. Identify students who critique their partner’s work and offer clear reasons for why the work is incorrect.
Answers
- The figure is a rectangle with vertices at (2,2), (2,4), (−3,4), and (−3,2).
- Possible description: The figure is a rectangle. The sides are parallel to the x- and y-axes. The lower-left vertex is located at (−3,2). The width is 5 units and the height is 2 units.
Work Time
Name the Figure
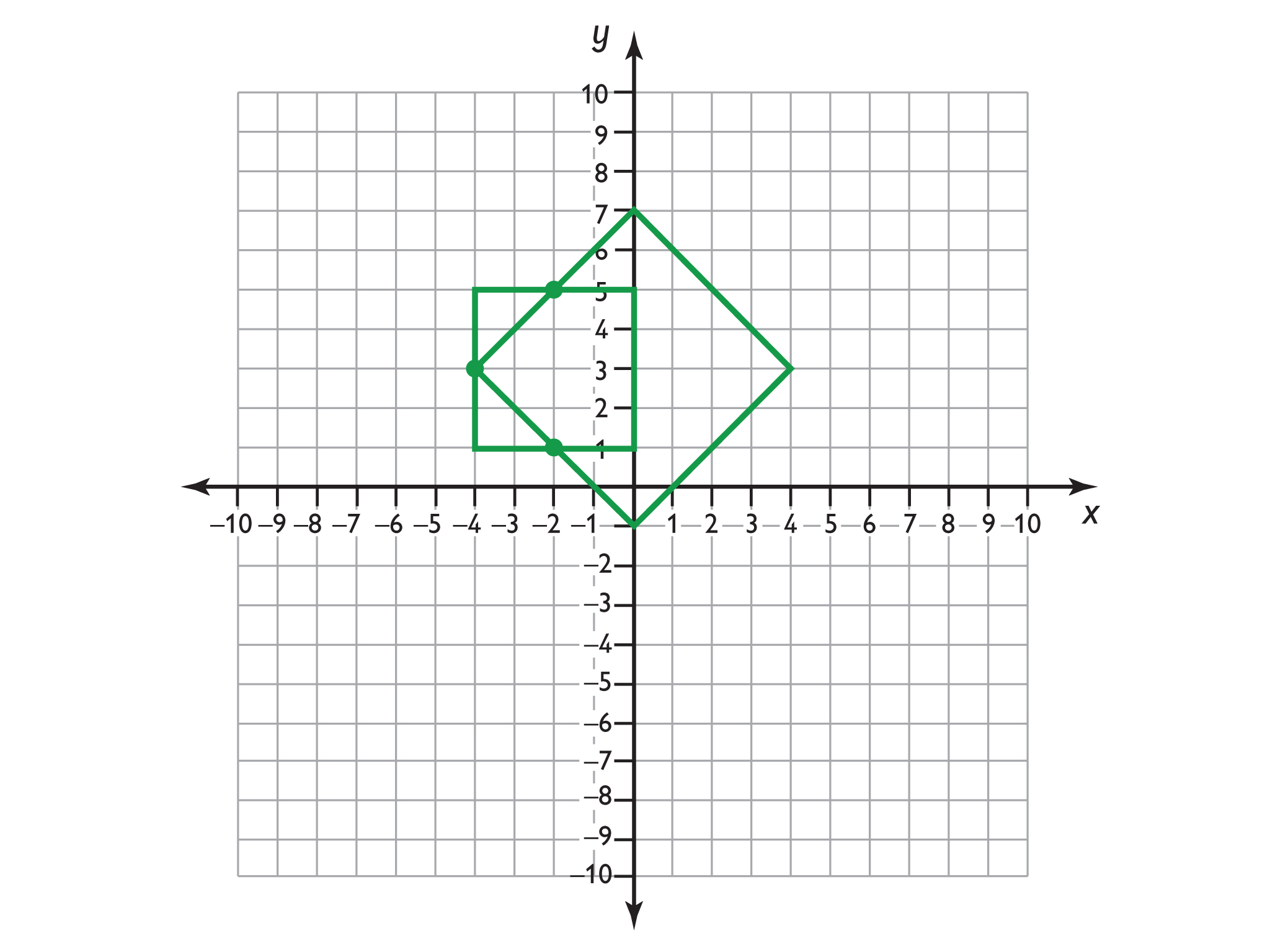
Look at this figure.
- Name the figure and the location of its vertices on the coordinate plane.
- Without providing coordinates of all four vertices, write a description that describes this figure. Someone who has not seen this figure should be able to duplicate it from your description.
Ask yourself:
- Look at the sides and the angles of the figure. What figure has these characteristics?
- Are the sides parallel or perpendicular to either the x - ory -axis?
- What are the coordinates of one vertex?
- How long is the figure’s height?
- How long is the figure’s width?
Prepare a Presentation
Lesson Guide
Presentations can be prepared individually or with a partner.
Challenge Problem
Possible Answer
- There are many other possible squares tilted at 45 degrees, and many other possibilities tilted at angles other than 0 degrees or 45 degrees.
- A circle where these points are on the circumference.
Work Time
Prepare a Presentation
- Describe the process you went through to draw the square figure.
- Describe how you made sure that your description of the rectangle was simple yet did not describe any other figure on the coordinate plane.
Challenge Problem
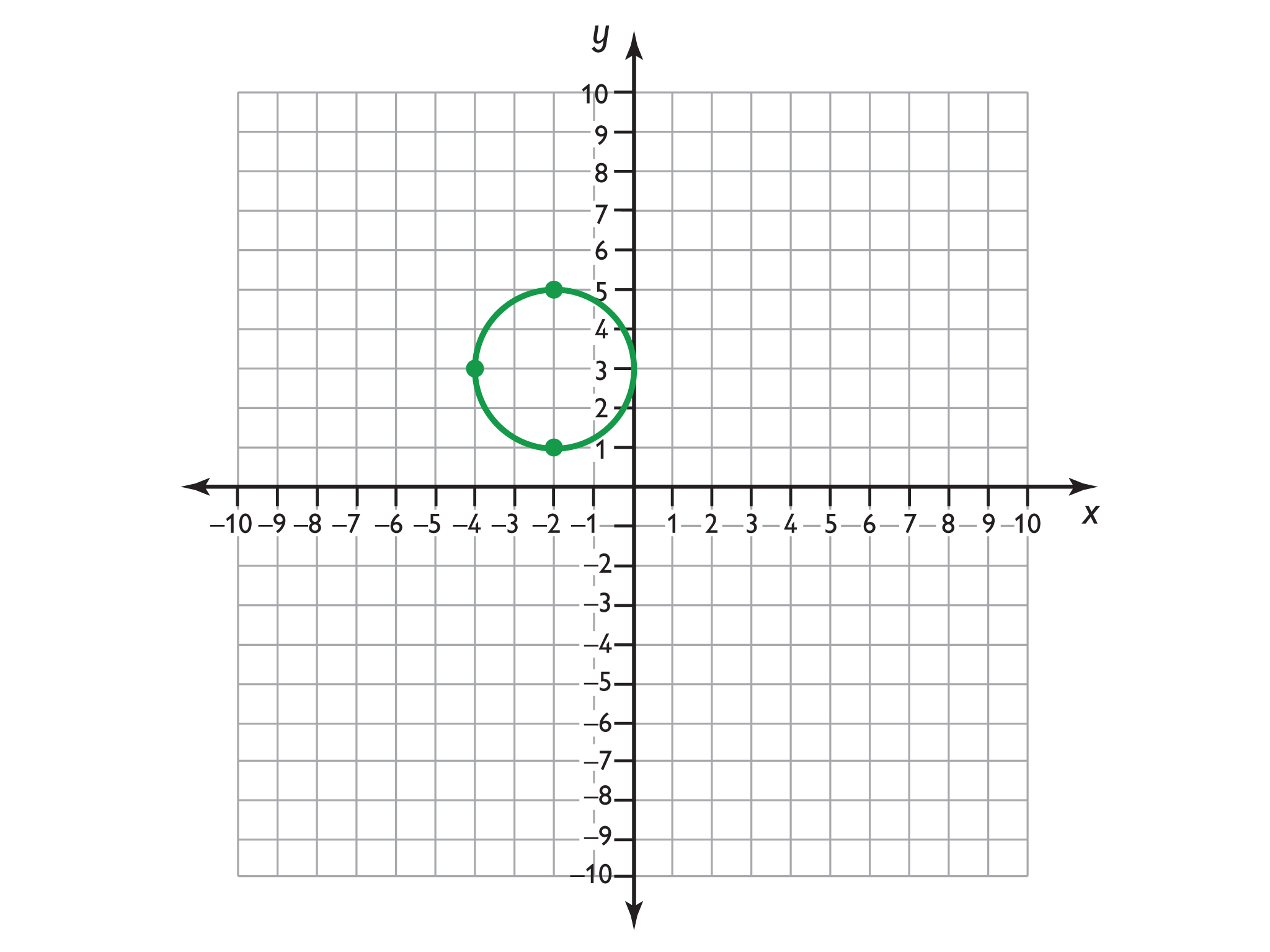
- Find a square that includes all the points on the sides of the square.
- Now, find two different squares that include the points.
- Sketch a circle where these three points are on the circumference.
Make Connections
Lesson Guide
Have students share their answers to the square problem. Check that students’ descriptions are clear and accurate.
Ask:
- What strategy did you use to draw the square?
- Did you and your partner use the same strategy?
- Why is it important to follow the description precisely?
- Is there more than one correct way to draw the square?
Have students share their answers to the rectangle problem. As students show their solutions, ask:
- How did you write a description for this figure?
- Did anyone use a different strategy? How is your method different?
- Is there any other figure that fits this description?
- Are there things you could leave out of your description and still have a description that is not a description of any other figure?
Have students give their presentations. Ask questions such as these:
- What did you like about [Name]’s presentation?
- How did [Name]’s presentation compare to [Name]’s presentation?
- How are they similar?
- How are they different?
- Whose presentation makes more sense to you? Why?
Have students who did the Challenge Problem share their work.
In the discussion, elicit that there are an infinite number of squares that have these points on their sides, but there is only one circle that has these points on its circumference.
SWD: During the presentations, provide some students with a note-taking organizer that includes a space for:
- The presenters’ names
- The presenters’ answers to the problem
- The presenters’ explanations of the mathematics
- The student’s summary of the presentations in his or her own words
- Reflection on what was presented (How were the presentations similar or different?)
This will help students when they reflect on the presentations.
ELL: Be sure that all ELLs participate in the presentation exercise, and monitor that ELLs do not shy away from this activity. Encourage the rest of the students to be patient if the pace of ELLs is slower than that of native speakers.
Performance Task
Ways of Thinking: Make Connections
Take notes about drawing figures on the coordinate plane.
As your classmates present, ask questions such as:
- What strategy did you use to solve the problem?
- How is your method different from the other methods mentioned so far?
- Why is it important to be precise when writing descriptions?
- Can you omit any part of the description and still get the same unique figure?
Figures on the Coordinate Plane
Possible Summary
You can use ordered pairs to name the vertices of a figure. You can include properties of the figure to distinguish it from other figures. You can include the length of the sides.
Formative Assessment
Summary of the Math: Figures on the Coordinate Plane
Write a summary of how you would describe a figure on the coordinate plane.
Check your summary.
- Do you explain what an ordered pair is?
- Do you explain how ordered pairs can be used to describe figures on the coordinate plane?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out how students can tell if they drew a figure that matches a description.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
The way I can tell if I drew a figure that matches a description is …