- Author:
- Pearson
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Education Standards
Area of a Trapezoid
Parallelogram
Parallelogram
Trapezoid
Analyzing The Formula of A Parallelogram & Trapezoid

Overview
Lesson Overview
Students find the area of a parallelogram by rearranging it to form a rectangle. They find the area of a trapezoid by putting together two copies of it to form a parallelogram. By doing these activities and by analyzing the dimensions and areas of several examples of each figure, students develop and understand area formulas for parallelograms and trapezoids.
Key Concepts
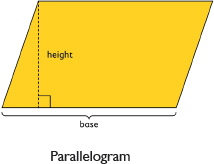
A parallelogram is a quadrilateral with two pairs of parallel sides. The base of a parallelogram can be any of the four sides. The height is the perpendicular distance from the base to the opposite side.
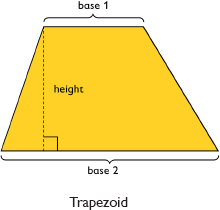
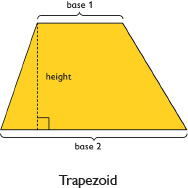
A trapezoid is a quadrilateral with exactly one pair of parallel sides. The bases of a trapezoid are the parallel sides. The height is the perpendicular distance between the bases.
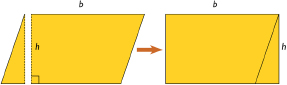
You can cut a parallelogram into two pieces and reassemble them to form a rectangle. Because the area does not change, the area of the rectangle is the same as the area of the parallelogram. This gives the parallelogram area formula A = bh.
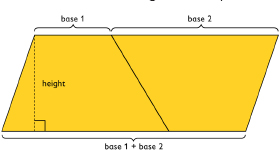
You can put two identical trapezoids together to form a parallelogram with the same height as the trapezoid and a base length equal to the sum of the base lengths of the trapezoid. The area of the parallelogram is (b1 + b2)h, so the area of the trapezoid is one-half of this area. Thus, the trapezoid area formula is A = 12(b1 + b2)h.
Goals and Learning Objectives
- Develop and explore the formula for the area of a parallelogram.
- Develop and explore the formula for the area of a trapezoid.
Introduction to Parallelograms
Lesson Guide
Review the definition of parallelogram with students.
Then have students watch the video and work in pairs to determine the formula for the area of a parallelogram.
SWD: Make sure that students know the characteristics of a parallelogram. Students may benefit from a concept web or polygon “family tree” that delineates the characteristics of different shapes.
Opening
Introduction to Parallelograms
A parallelogram is a quadrilateral that has two pairs of parallel sides.
The base of a parallelogram can be any side.
The height is the perpendicular distance from the base to the opposite side.
- Watch the video.
- Using what you know about the area of a rectangle, make a prediction about the formula for the area of a parallelogram.
VIDEO: Area of a Parallelogram
Introduction to Trapezoids
Lesson Guide
Review the definition for trapezoid with students.
Then have students watch the video and work in pairs to determine the formula for the area of a trapezoid.
Opening
Introduction to Trapezoids
A trapezoid is a quadrilateral with exactly one pair of parallel sides.
The bases of a trapezoid are the parallel sides.
The height is the perpendicular distance between the bases.
- Watch the video.
- Using what you know about the area of a parallelogram, determine the formula for the area of a trapezoid.
VIDEO: Area of a Trapezoid
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore the formula for the area of a parallelogram and the area of a trapezoid.
SWD: Generalization of skills can be particularly challenging for some students with disabilities. Students may need direct instruction on the connection between what they already understand and a general formula for the area of a parallelogram or trapezoid.
Opening
Explore the formula for the area of a parallelogram and the area of a trapezoid.
Areas of Parallelograms
Lesson Guide
Have students work with partners and use the Parallelogram interactive to answer the questions.
SWD: Students with disabilities, especially those with visual spatial difficulties and/or fine motor challenges, may benefit from adaptive tools (digital or in-hand) to complete this task. Consider providing paper cutouts of the parallelogram and trapezoid if your students will benefit from using concrete manipulatives.
Mathematical Practices
Mathematical Practice 1: Look for and make use of structure.
Identify students who understand how the operations in the formula impact the answer (i.e., increasing a factor increases the product; decreasing a factor decreases the product; or keeping the factors the same does not change the product).
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Watch for students who, through repeated trials, reason that if one variable is constant and the other variable increases (or decreases), then the area increases (or decreases) as well.
Look for students who, through repeated trials, reason that if both variables remain constant, the area remains constant as well.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What does it mean to keep the height or base constant?
- How can you change the height (the base) using the interactive?
- How can you change one of the angles but keep the height and the base the same?
Student changes the variable only one way, just increasing (or decreasing) its value.
- Can you decrease (or increase) the length of the base? What happens?
- Can you decrease (or increase) the height? What happens?
Student works unsystematically.
- How can you record your observations?
- Work on one question at a time and record what you observe.
Student has a correct solution.
- How did you reach your conclusion?
- Explain how the Parallelogram interactive helped you reach a conclusion.
Possible Answers
- Answers will vary. Possible answer: If the height is constant and I decrease the base, the area decreases. If the height is constant and I increase the base, the area increases.
- Answers will vary. Possible answer: If the base is constant and I decrease the height, the area decreases. If the base is constant and I increase the height, the area increases.
- If the height and base remain constant and I change one of the angles, the area of the parallelogram does not change.
Work Time
Areas of Parallelograms
The formula for the area of a parallelogram is:
area = base • height, or A = bh
Use the Parallelogram interactive to explore the area of a parallelogram. Move the vertices of the parallelogram and explore what happens to the area.
- What happens if you keep the height constant and change the base?
- What happens if you keep the base constant and change the height?
- What happens if you keep the height and base constant and change one of the angles?
INTERACTIVE: Parallelogram
Hint:
To increase the height, move the top side farther away from the base.
Areas of Trapezoids
Lesson Guide
Have students work with partners and use the Trapezoid interactive to answer the questions. Then have partners work on their presentations.
Mathematical Practices
Mathematical Practice 1: Look for and make use of structure.
Identify students who understand how the operations in the formula impact the answer (i.e., increasing a factor increases the product; decreasing a factor decreases the product; or keeping the factors the same does not change the product).
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Watch for students who, through repeated trials, reason that if one variable is constant and the other variable increases (or decreases), then the area increases (or decreases) as well.
Look for students who, through repeated trials, reason that if both variables remain constant, the area remains constant as well.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What does it mean to keep the height or base constant?
- How can you change the height (the base) using the interactive?
- How can you change one of the angles but keep the height and the base the same?
Student changes the variable only one way, just increasing (or decreasing) its value.
- Can you decrease (or increase) the length of the base? What happens?
- Can you decrease (or increase) the height? What happens?
Student works unsystematically.
- How can you record your observations?
- Work on one question at a time and record what you observe.
Student has a correct solution.
- How did you reach your conclusion?
- Explain how the Trapezoid interactive helped you reach a conclusion.
Possible Answers
- Answers will vary. Possible answer: If the height is constant and I decrease one of the bases, the area decreases. If the height is constant and I increase one of the bases, the area increases.
- Answers will vary. Possible answer: If the bases are constant and I decrease the height, the area decreases. If the bases are constant and I increase the height, the area increases.
- If the height and bases remain constant and I change one of the angles, the area of the trapezoid does not change.
Work Time
Areas of Trapezoids
The formula for the area of a trapezoid is:
area = (base 1 + base 2) • height, or A = (b1 + b2)h
Use the Trapezoid interactive to explore the area of a trapezoid. Move the vertices of the trapezoid and explore what happens to the area.
- What happens if you keep the height constant and change one of the bases?
- What happens if you keep the bases constant and change the height?
- What happens if you keep the height and bases constant and change one of the angles?
INTERACTIVE: Trapezoid
Prepare a Presentation
Lesson Guide
Student conclusions and explanations will vary.
Preparing for Ways of Thinking
As students work on the problems, look for the following examples to share in the Ways of Thinking discussion:
- Students who recognize that if one variable is constant, increasing (or decreasing) the other variable also increases (or decreases) the area
- Students who understand that if the height and base are constant and one angle changes, the area remains constant
- Students who recognize that if the base (or height) of the parallelogram increases (or decreases) by a factor, then the area increases (or decreases) by the same factor
- Students who recognize that if the height of the trapezoid increases (or decreases) by a factor, then the area increases (or decreases) by the same factor
- Students who reason that if one of the bases of the trapezoid increases (or decreases), the area increases (or decreases), but not by the same factor
- Students who do not see a relationship between height, base, and area
- Students who recognize the relationship between the formula for the area of a parallelogram and the area of a trapezoid: since b1 = b2 in a parallelogram, then A =(b1 + b2)h = (b1 + b1)h = b1h.
ELL: Encourage students to use the academic vocabulary they are learning. When ELLs participate in the discussion, monitor for knowledge of the topic. Follow up on statements that seem unclear. When ELLs contribute, focus on content and don't allow grammar difficulties to distract you from understanding the meaning (as much as possible). Help ELLs who make grammar mistakes by rephrasing, but ensure your rephrasing does not interrupt or interfere with their thinking.
Challenge Problem
Answers
- Presentations will vary. Possible answer: As the pair of opposite sides slide in opposite directions, the area will stay the same.
- Even though the parallelograms have different shapes, the base and the height stay the same. Because the area of a parallelogram equals the base times the height, the area also will not change.
Work Time
Prepare a Presentation
- Select one of your conclusions about what happens to the area of a parallelogram or a trapezoid when you change one or more variables.
- Be prepared to demonstrate your conclusion using the Parallelogram or Trapezoid interactive, and to support your thinking mathematically.
Challenge Problem
Suppose you start with a parallelogram and then slide a pair of opposite sides in opposite directions along parallel lines.
- Predict how the area will change. Use the Parallelogram interactive to test your prediction.
- Support your prediction with data from the Parallelogram interactive.
INTERACTIVE: Parallelogram
Make Connections
Mathematics
Have student pairs present their work. Be sure to include the work of students who had trouble along the way and those who developed incorrect conclusions, as all students can benefit from the discussion. Test students' conclusions using the Parallelogram and Trapezoid interactives to verify if the statements are accurate.
Have students who did the Challenge Problem share their thinking. Ask class members to evaluate if their thinking makes sense.
Performance Task
Ways of Thinking: Make Connections
- Take notes about classmates’ conclusions concerning what happens to the area of a parallelogram or a trapezoid when you change one or more variables.
Hint:
As your classmates present, ask questions such as:
- What surprised you in your exploration of parallelograms?
- What surprised you in your exploration of trapezoids?
- How does your exploration of parallelograms compare to your exploration of trapezoids? What is the same and what is different?
Area of Parallelograms and Trapezoids
A Possible Summary
You can move parts of a parallelogram around to make a rectangle. Once you have formed a rectangle, you can find its area. The formula for the area of a parallelogram is A = bh, where b is the base and h is the height.
You can make a copy of a trapezoid, put the two trapezoids together to make a parallelogram, find the area of the parallelogram, and take half of that area to get the area of the original trapezoid. The formula for the area of a trapezoid is A = (b1 + b2)h where b1 is one base, b2 is the other base, and h is the height.
ELL: ELLs will understand more of what you say if you remember to modify your language as needed. Find subtle but effective ways to check that students have understood.
- Use shorter, less complex sentences for beginning ELL students.
- Avoid pronouns.
- Emphasize nouns and verbs.
- Use simple sentence structures.
- Use intonation, volume, and pauses to help make the meaning clear.
- Rephrase instead of repeating.
- Paraphrase important concepts and directions.
Formative Assessment
Summary of the Math: Area of Parallelograms and Trapezoids
- Write a summary of what you learned about the area of parallelograms and trapezoids.
Hint:
Check your summary:
- Do you provide the area formulas for a parallelogram and a trapezoid with explanations of what each variable represents?
- Area of a parallelogram = bh
- Area of a parallelogram = h(b1+b2)2
- Do you include sketches or written descriptions showing how you found the formulas?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to learn what surprised students about the area of parallelograms and trapezoids.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One thing that surprised me about the area of parallelograms and trapezoids was …