- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Downloadable docs, Text/HTML
Shoes and Socks Reflection
Summary Preparation

Overview
Students discuss classroom routines and expectations, work with partners to present their work matching different representations of a ratio situation, and then prepare math summaries.
Introduce classroom routines and expectations prior to the full mathematics lesson. Ask students to discuss how to clearly present their work to their classmates. Model an example of partner work, and then have students work with their partners to match different representations of a ratio situation. Read and discuss a Summary of the Math, and then have students write Reflections about their wonderings.
Key Concepts
Students match a data card with its corresponding ratio, decimal, fraction, percent, and description of the relationship in words. Students construct viable arguments for their matches and critique the reasoning of their partner and other classmates.
Goals and Learning Objectives
- Describe the classroom routines and expectations.
- Consider how to present work clearly to classmates.
- Collaborate with a partner.
- Critique a partner’s reasoning.
- Connect different representations of a ratio situation.
Lesson Routines
Lesson Guide
Thanks students for their effort during the last lesson.
Tell students that each lesson has a similar structure and typically follows these classroom routines:
- Opening sparks your thinking about the math in today’s lesson.
- Work Time asks you to solve one or more problems on your own and with your partner.
- Ways of Thinking is a time for you and your classmates to present your mathematical thinking. As a class, you will discuss the different mathematics you and your classmates used to solve the problems.
- Apply the Learning is a chance for you to work on your own and apply the mathematics you just learned.
- Summary of the Math has you pull together your ideas about today’s math after the Ways of Thinking discussion.
- Reflection involves looking back on today’s lesson and looking forward to future lessons to write questions or ideas that you are still wondering about.
- Exercises give you an opportunity to work through other problems that build on the mathematics of today’s lesson.
Tell students that they will complete all of their work in their Notebook. They should save all their work, because what they record, even mistakes, represents their thinking. Thinking cannot be erased—it can only be revised and improved upon. Explain that students will also have the opportunity to show their revised work in the Notebook.
Opening
Lesson Routines
In each lesson, you have the same routines.
- Read through the list of routines.
- Listen as your teacher explains what you will do during each routine.
Classroom Expectations
Lesson Guide
Discuss these classroom expectations:
- The procedure for gathering materials as students enter the room, including the technology they will be using
- The routine for submitting exercises, with regard to when and how
- The procedure for obtaining any additional materials needed for the lesson
- The procedure and locations for putting away materials at the end of the lesson
- Any other routines or habits that fit with the classroom norms that the class established and will help the class run more smoothly
Share this list of classroom expectations with the class, or ask students to complete a graphic organizer in their Notebook summarizing the information. A poster in the room might also be helpful because many of these classroom expectations are relevant for every lesson.
Opening
Classroom Expectations
These are our classroom expectations.
Discuss them with your classmates.
- As I enter the classroom, I am expected to…
- I am expected to submit exercises before…
- To get the technology and any additional materials, I am expected to…
- To put away materials at the end of the lesson, I am expected to…
- I am also expected to…
Qualities of Effective Presentations
Lesson Guide
Explain that during Work Time, students will often prepare a presentation illustrating their ways of thinking about the mathematics in the lesson. Ask students to consider these questions:
- How do you organize your work to clearly communicate your thinking about a problem?
- What kinds of visuals are helpful?
- How can you make sure you explain your strategies and reasons well?
Have students spend a few minutes thinking about these three questions on their own. Then have students discuss their ideas with their partner.
When students are done, have them share their ideas with the class. As with the classroom norms, when students generate their own ideas, they take ownership of their own learning.
These Hints for students are ideas about how to prepare clear presentations:
- Understand your own work.
- Use visuals and gestures to help others know what you are talking about.
- Say fewer words and choose them carefully.
- Include diagrams and graphs when appropriate.
- Speak clearly and slowly.
- Stay calm. Remember to breathe.
- Listen carefully to comments and questions.
- Pause to think about your response before speaking.
Record the ideas as you project them for the class. After all ideas are listed, review each one for clarity. Agreement is not necessary because diversity in presentation styles can be beneficial. This list should grow over the year.
Opening
Qualities of Effective Presentations
During Work Time, you often prepare a presentation.
Discuss the following with your classmates.
- How do you organize your work to clearly communicate your thinking about a problem?
- What kinds of visuals are helpful?
- How can you make sure you explain your strategies and reasoning well?
Hint:
Here are ideas about how to prepare clear presentations:
- Understand your own work.
- Use visuals and gestures to help others know what you are talking about.
- Say fewer words and choose them carefully.
- Include diagrams and graphs when appropriate.
- Speak clearly and slowly.
- Stay calm. Remember to breathe.
- Listen carefully to comments and questions.
- Pause to think about your response before speaking.
Model Partner Work
Lesson Guide
Have students watch the example of how to complete a card sort with a partner.
Teacher Demo
Tell students that they will often work with a partner during class. Today, students will work with a partner to match different representations of a ratio situation.
Have a student read the instructions aloud.
Then model working with a partner by turning to a student and asking him or her to be your partner. Work on the card sort and explain each step as you model it.
- Find two cards that match.
- Explain to your partner why the cards match. Have your partner ask questions if he or she is unclear about your reasoning.
- Ask your partner to find two cards that match and explain his or her reasoning to you. Ask questions if your partner's explanation is unclear.
- Continue matching cards until all the cards for the same store are in a set.
Model the idea that after partners explain their ideas to each other, they should use any time that remains to clarify their work as they prepare their presentation.
Opening
Model Partner Work
Watch your teacher demonstrate how to complete this task with a partner.
- Take turns matching cards that represent the same footwear store.
- Explain to your partner how you know the cards match. Challenge your partner to have clear and complete explanations.
- Continue matching cards until all the cards for the same store are in a set.
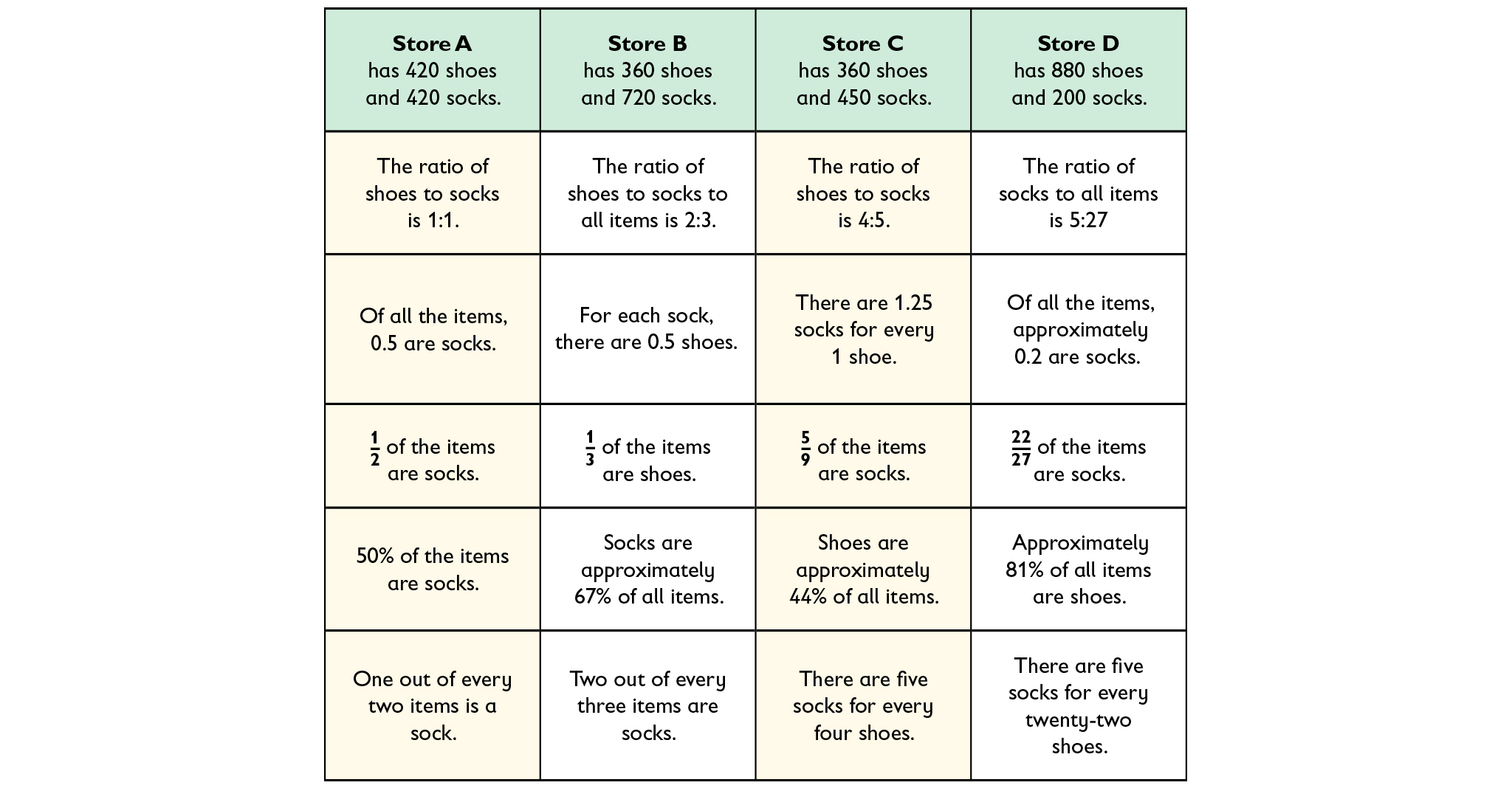
HANDOUT: Shoes and Stockings: Comparing Ratios
Math Mission
Lesson Guide
Discuss the Math Mission. Students will connect different representations of equivalent ratios.
Opening
Connect different representations of equivalent ratios.
Match Representations of Ratios
Lesson Guide
Have students work with their partner and take turns matching different representations of equivalent ratios.
Tell students to complete all of their work in their Notebook. They should save their work—even if it includes mistakes. Explain that mistakes represent their thinking. Thinking cannot be erased—it can only be revised and improved upon. Tell students that they can create a new page in their Notebook to show their corrected work.
ELL: When listening to students' responses, give students advance notice that they will be presenting their work on a specific problem during the Ways of Thinking section. This will give them ample time to prepare a thoughtful response.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Students engage in productive partner dialog by presenting their explanations and critiquing each others' reasoning.
Interventions
Student has difficulty recognizing that some representations describe the part-to-part ratio in the situation and others show the part-to-whole ratio.
- How is the order important in ratio representations?
- Can you write a different fraction about that store’s ratio of shoes to socks?
Student is confused about why there are different kinds of representations for ratios.
- Which representation of the ratio is easiest for comparing the ratio of socks to items in the store?
- Talk with your partner about how the different representations give you different information about the store.
Answers
- Ratio Card Sort solution:
Work Time
Match Representations of Ratios
Work with your partner.
- Take turns matching cards that represent the same footwear store.
- Explain to your partner how you know the cards match. Challenge your partner to have clear and complete explanations.
- Continue matching cards until all the cards for the same store are in a set.
HANDOUT: Shoes and Socks Reflection
Hint:
- How is the ratio of socks to shoes different than the ratio of socks to all items?
- Think about whether the ratio describes the relationship between parts or between the part and the whole.
- You can write a ratio as a fraction or a decimal using division.
Prepare a Presentation
Lesson Guide
Have students prepare a presentation that describes their strategies for matching different representations of a ratio situation. Remind students to think about the qualities of an effective presentation. If they would like to, students can refer to the Hints previously shared/posted about how to prepare a clear presentation.
Preparing for Ways of Thinking
As students work, walk around the room and listen carefully to their reasoning. Watch for these things:
- Is the listener asking questions when the speaker is unclear?
- Do both partners explain their processes, even if they each did something similar?
- Do students understand how the representations are related?
Select several student pairs to present one of their card matches and their explanation. Ask students who correctly and incorrectly matched the cards to present, especially students who show the common issues identified in Interventions.
You may want to order the presentations to focus the discussion on one representation at a time (decimals, percent, and so forth). Start with the representation that students understand the best and then continue with those ratio representations with incorrect matches. By the end of the presentations, students should understand all the different representations of the ratio situation.
Challenge Problem
Possible Answers
- The ratio of shoes to socks in this footwear store is 4 to 3.
- The ratio of socks to shoes is 0.75.
- 4/7 of all items are shoes.
- Approximately 43% of the items are socks.
Work Time
Prepare a Presentation
Focus on the set that was hardest to match.
- Describe your strategies for matching the ratio cards.
- Explain your reasoning and justification.
- Identify any mistakes you made and what you learned from them.
- Include any questions your partner asked about your explanation.
Challenge Problem
Another footwear store has 1,800 shoes and 1,350 socks.
- Write the simplified ratio of shoes to socks.
- Write a decimal for the ratio of socks to shoes.
- Write a fraction for the ratio of shoes to all items.
- Write a percent for the ratio of socks to all items.
Make Connections
Lesson Guide
Have the students you identified during Preparing for Ways of Thinking share their presentations. Remind students about the ways you expect them to react to any mistakes:
- Ask clarifying questions.
- Explain reasons for disagreeing with the answers.
- No laughing or teasing.
- Use mistakes as an opportunity to learn.
As students watch the presentations, ask them to take notes about how their own strategy for solving the problem is similar to and different from the presenters’ strategies. Students should look for new ideas they might want to try themselves. Encourage students to ask questions about the presenters’ thinking to better understand the different mathematical ideas.
Have presenters explain how they know the cards match, and explain why they found those cards the most difficult. Make links between their different approaches and highlight the variability in the strategies that students used.
Mathematics
Focus the class discussion on the advantages of the different kinds of representations and how a particular representation may be appropriate in certain situations (for example, percents).
Ask students:
- How are the different representations similar and different from each other?
- Which representation is most helpful in picturing the footwear store? Which makes it easier to compare the stores to each other?
- What are the different parts in the ratio situation? What is the whole?
- Is it easier for you to understand a fraction, a decimal, or a percent?
- Why are the ratios from the same store not equivalent?
Ask a few students who completed the Challenge Problem to present their ratio representations for the new store. Ask students to explain how they figured out the different ratio representations.
Have partners share with the class an example of justifying and critiquing others' reasoning. Partners should either summarize their work for the class or explain their disagreement and how they resolved it.
The Hints help model productive questions for students to ask during Ways of Thinking. You can see these sample questions by opening the Hints on the student screen.
Performance Task
Ways of Thinking: Make Connections
- Take notes about how your own thinking is similar to and different from your classmates’ thinking.
- Are there new ideas that you want to try out?
- What critiques do you have about your classmates’ ways of thinking?
Hint:
As your classmates present, ask questions such as:
- What words helped you know if it was a part-to-part or part-to-whole ratio?
- Did you find it harder to match the decimals, the fractions, the ratios, or the percents?
- Where did you include your strategy and explanation in your presentation?
- Are there any visuals that would be helpful to add to your presentation?
Represent Ratios
Lesson Guide
Tell students that for most lessons, they will summarize what they learned after Ways of Thinking. During Summary of the Math, students will either individually write a summary of the mathematical concepts of the lesson or read and discuss a summary as a class. Today the class will read and discuss a summary together.
Mathematics
First, have partners read and discuss the summary together for a few minutes. Then ask the class:
- What does it mean that there are two quantities in a ratio?
- How do you change a fraction to a decimal or a percent, or vice versa?
- How are part-to-part ratios and part-to-whole ratios different?
- Are there other things that might be useful to add to this summary?
As a class, add any additional details that students thought were important. When you are finished, record and share the summary with the class. Students can refer to this summary during future lessons as a reminder of key mathematical concepts.
Formative Assessment
Summary of the Math: Represent Ratios
Read and Discuss
- A ratio is the comparison of two quantities by division.
- A ratio can be expressed as a fraction, a decimal, or a percent.
- Ratios can compare a part to a part or a part to a whole.
Hint:
Can you:
- Write a ratio as a fraction if it is given as a decimal?
- Determine whether a ratio is a part-to-part or a part-to-whole comparison?
- Explain how you know what the ratio is comparing?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class.
Discuss that reflections are a time for students to write questions or wonderings that have arisen during the lesson. Students should reflect on questions such as these:
- What are you curious about?
- What would you like to pursue further in a different way?
Review the reflections to see what things students wonder about ratios. Record any wonderings and share with the class as appropriate.
SWD: Some students with disabilities may struggle to explain their mathematical reasoning in words. Provide sentence starters or paragraph frames to support students with this task.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use this sentence starter below if you find it to be helpful.
Something I wonder about ratios is…