- Author:
- Pearson
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Exploring the Great Lakes
Exploring the Great Lakes
Great Lakes
Thinking About Lake Ontario
Interpreting Graphs & Diagrams

Overview
How much water is in the Great Lakes? Students read and interpret a diagram that shows physical features of the Great Lakes and answer questions based on the diagram. They find the volume of each of the Great Lakes, as well as all five lakes combined, and make a bar graph to represent the volumes.
Key Concepts
Students are expected to use the mathematical skills they have acquired in previous lessons or in previous math courses. The lessons in this unit focus on developing and refining problem-solving skills.
Students will:
- Try a variety of strategies to approaching different types of problems.
- Devise a problem-solving plan and implement their plan systematically.
- Become aware that problems can be solved in more than one way.
- See the value of approaching problems in a systematic manner.
- Communicate their approaches with precision and articulate why their strategies and solutions are reasonable.
- Make connections between previous learning and real-world problems.
- Create efficacy and confidence in solving challenging problems in a real-world setting.
Goals and Learning Objectives
- Read and interpret graphs and diagrams.
- Solve problems involving volume.
The Great Lakes
Lesson Guide
Have students refer to the map of the Great Lakes as you explain that the Great Lakes are a collection of five freshwater lakes in northeastern North America on the border of the United States and Canada. The Great Lakes form the largest group of freshwater lakes on Earth, comprising about 21% of the world's surface fresh water. See if students can name the five Great Lakes: Lake Erie, Lake Ontario, Lake Michigan, Lake Huron, and Lake Superior.
Have students discuss the following question with a partner for 1 to 2 minutes:
- How big do you think the Great Lakes are?
Next, discuss the question as a class. Elicit the point that more information is needed to calculate the area of the surfaces of all the lakes combined.
ELL: Use a concept map with Great Lakes in the center. This will allow ELLs to visually organize their prior knowledge around what they know about the Great Lakes.
Mathematics
Emphasize that students need more information about the Great Lakes to find the total area of all the surfaces of lakes combined. Ask these guiding questions:
- What information is needed to find the area of each lake?
- What information is given in the map?
- What additional information do you need?
SWD: Students will need to apply formulas for area, surface area and volume. Create ways to help students with disabilities to recall the formulas necessary (without over scaffolding the task). For example, provide partial formulas such as A = b_ or V = B_. Have students complete it prior to doing the calculations necessary to answer the questions.
Opening
The Great Lakes
How big do you think the Great Lakes are? To get an idea, open the Great Lakes interactive and drag the Great Lakes to the state of your choice.
- Estimate which has a greater surface area, the Great Lakes or the state of your choice.
- Estimate the surface area of all the Great Lakes combined.
After you’ve made your estimates, explain your thinking to your partner.
Discuss the following with your classmates.
- What information do you need to know in order to calculate the volume of water in the Great Lakes?
- How would you go about finding that information?
INTERACTIVE: Great Lakes
Problem-Solving Process
Lesson Guide
Before students begin, review the steps of the problem-solving process with the class:
Problem-Solving Steps
- Understand the problem situation.
- What is the problem asking you to find out?
- What information is provided?
- What are the quantities that vary?
- How are the variables related?
- Represent the situation.
- Answer the question.
- Check that the mathematical answer makes sense.
- Prepare a presentation.
Opening
Problem-Solving Process
Discuss and use the problem-solving process with your classmates as you solve today's problems.
Problem-Solving Process
- Understand the problem situation.
- Represent the situation.
- Answer the question.
- Check that the mathematical answer makes sense.
- Prepare a presentation.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will analyze diagrams, interpret information, and create a strategy to determine the Great Lakes' water volume.
ELL: After you have reviewed the formulas for area and volume. Create an anchor chart that contains all the formulas students will need for calculating area, surface area, or volume.
Opening
Math Mission
Analyze diagrams, interpret information, and create a strategy to determine the Great Lakes' water volume.
Explore the Great Lakes
Lesson Guide
Have students work independently to start. During independent time, observe students working, but refrain from asking guiding questions or giving students hints. Give students the opportunity to organize their problem-solving plans and the information given in the problem independently before asking others for assistance.
After independent work time, allow students to work with a partner to complete the problems. Have partners share their problem-solving plans. Partners should agree on a plan and work together to find the solutions. During this time, circulate around the classroom asking guiding questions and noting strategies you want students to share during the class discussion.
SWD: Consider the prerequisite skills for this lesson. Students with disabilities may need direct instruction and/or guided practice with the skills needed to complete the tasks in this lesson. Pull individual students and/or a small group for direct instruction or guided practice for converting feet to miles.
Possible Answers
- Depending on which view is used, the vertical scale could represent surface elevation, average depth, or maximum depth.
- The 0 on the vertical axis represents sea level.
- The elevation and depths are surface elevation, average depth, and maximum depth. The surface elevation is the elevation of the lake at the water's surface. The average depth is the average depth of the water in each lake. The maximum depth is the greatest depth of each lake.
- Each blue area represents the volume of water for each lake. Lake Superior has the greatest volume of water; Lake Erie has the least volume of water.
Work Time
Explore the Great Lakes
Use the Exploring the Great Lakes interactive to explore the Surface Elevation, Average Depth and Maximum Depth of the Great Lakes
- What does the vertical scale, ranging from –1,000 to 600, represent?
- What does 0 on the vertical axis represent?
- Elevation and depths are shown for each lake. Explain the meaning of each elevation and depth.
- What does each blue area in the diagram represent? Can you tell which lake has the greatest volume and which has the least volume?
INTERACTIVE: Exploring the Great Lakes
Volume of the Great Lakes
Lesson Guide
Continue as in Task 4.
SWD: During Partner Work, monitor student discussions and provide guiding questions from the Intervention section in writing to help students see the mathematics and find their own way to a solution. If a student is struggling with a particular concept, hold an individual conference. If many students are struggling with a concept, pull a small group to discuss the concept.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students must make sense of the data presented in the diagram as well as the table to calculate the volume of each lake. They need to persevere in using this data to complete their solutions.
Mathematical Practice 2: Reason abstractly and quantitatively.
Students reason abstractly to make sense of each type of depth presented in the Great Lakes interactive. They use this diagram to make sure their calculations are reasonable since the area of each rectangle on the diagram is proportional to the volume of each lake. Student reason quantitatively when using numerical values in both the diagram and the table to calculate the volume of each of the Great Lakes. They need to decide which type of depth (average, surface, or maximum) is necessary to calculate the volume accurately.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students construct arguments regarding why their answer is reasonable, and they have the opportunity to critique the reasoning of others during the class discussion.
Mathematical Practice 4: Model with mathematics.
Students use the diagram to determine the important information they need to solve this problem. Some students may present their responses using models and graphs.
Mathematical Practice 5: Use appropriate tools strategically.
Students use the tools provided (diagram and table) to synthesize the data needed to solve this problem. Students may also use other tools, such as calculators, while solving this problem.
Mathematical Practice 6: Attend to precision.
Students need to attend to precision while calculating the volume of each lake and understand the units presented in both the diagram and the table. They need to understand that in order to have precise answers, some conversions between units are necessary to solve this problem.
Mathematical Practice 7: Look for and make use of structure.
Students make use of the problem-solving processes while completing their solution.
Interventions
Student has difficulty getting started.
- What information is presented in the diagram? What types of depth are described?
- What information is presented in the table?
- What do you notice about the units for the measurements given in the table compared to the units for the measurements in the diagram?
- How can you convert feet to miles?
- What information is necessary to calculate volume?
Student has an answer, but it is incorrect.
- Do you need to convert any units when solving this problem?
- How can you use the area of the bars in the diagram to see if your answers are reasonable?
- What are cubic miles? Is your answer reasonable?
- Which type of depth (average, surface, or maximum) should you use to find the volume of the lake? Why?
Student has an answer but is having trouble articulating his or her thinking.
- What strategies did you use to solve this problem?
- How did you know you needed to perform unit conversions in your answer? How did you convert your units?
- How can you explain your reasoning to somebody who is struggling?
- Is your answer reasonable? How do you know?
Student has the correct answer and is waiting on others to finish.
- Use this data to create a Challenge Problem to share with your partner.
- How can you express your answer in cubic feet instead of cubic miles? Which unit makes more sense to use in this problem? Why?
- Is your answer exact or an estimate? Why?
- How are the lakes organized on the diagram?
Be sure to point out that the volumes students found are estimates instead of exact answers because they used the average depth of the lakes. Since the depth of the lakes is not consistent throughout, the average depth is a close marker for the depth of the lakes, but it is still an estimate.
Emphasize the importance of unit conversions from feet to miles or square miles to square feet when calculating the volume of each lake.
Point out any mathematical processes you observed during the work period.
Possible Answers
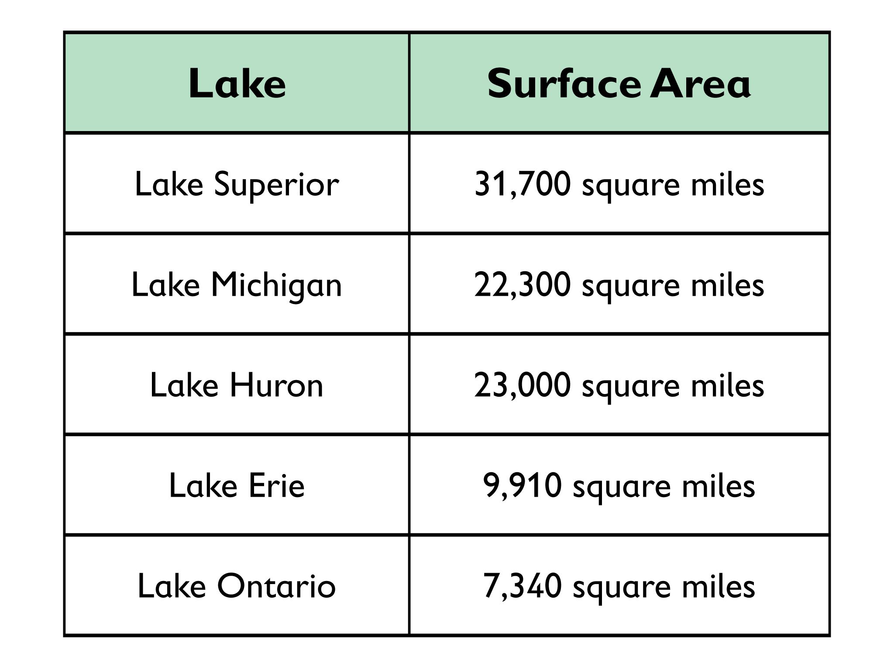
- Use the table to find the area of each lake, and then use the diagram to find the average depth of each lake. Since volume is the area of the base multiplied by the height, multiply the area of the lake by the average depth to estimate the volume of each lake.
- Possible solutions:
- Lake Superior: 483 ft ÷ 5,280 ft/mi ≈ 0.0915 mi
31,700 mi2 ⋅ 0.0915 mi ≈ 2,900 mi3
The approximate volume of Lake Superior is 2,900 mi3. - Lake Michigan: 279 ft ÷ 5,280 ft/mi ≈ 0.0528 mi
22,300 mi2 ⋅ 0.0528 mi ≈1,180 mi3 T
he approximate volume of Lake Michigan is 1,180 mi3. - Lake Huron: 195 ft ÷ 5,280 ft/mi ≈ 0.0369 mi
23,000 mi2⋅ 0 .0369 mi ≈ 879 mi3
The approximate volume of Lake Huron is 879 mi3. - Lake Erie: 62 ft ÷ 5,280 ft/mi ≈ 0.0117 mi
9,910 mi2 ⋅ 0.0117 mi ≈ 116 mi3
The approximate volume of Lake Erie is 116 mi3. - Lake Ontario: 283 ft ÷ 5,280 ft/mi ≈ 0.0536 mi
7,340 mi2 ⋅ 0.0536 mi ≈ 393 mi3
The approximate volume of Lake Ontario is 393 mi3.
- Lake Superior: 483 ft ÷ 5,280 ft/mi ≈ 0.0915 mi
- Possible solution: 2,900 + 1,180 + 879 + 116 + 393 = 5,468
The total volume of water in all the Great Lakes is approximately 5,468 mi 3. - Possible solution: 1,180 + 879 + 116 + 393 = 2,568
2,900 − 2,568 = 332
The total volume of water in Lake Michigan, Lake Huron, Lake Erie, and Lake Ontario is approximately 2,568 mi3. Since the volume of water in Lake Superior is approximately 2,900 mi3, all of the water from the four other Great Lakes would fit into Lake Superior with approximately 332 mi3 of space remaining.
Work Time
Volume of the Great Lakes
Use the table and Exploring the Great Lakes interactive to answer the following questions.
- How can you use the information from the table and Exploring the Great Lakes interactive to find the volume of each Great Lake? What information could you use from the interactive?
- What is the approximate volume of water in each Great Lake?
- What is the volume of water in all of the Great Lakes combined?
- Could all the water in Lakes Erie, Huron, Michigan, and Ontario fit in Lake Superior if Lake Superior was drained? If so, how much space would not be used? If not, how much water would spill out of Lake Superior?
Think about the diagram. Which measure of depth would you use to find the volume—the surface elevation, the average depth, or the maximum depth?
Lake Ontario
Lesson Guide
Continue as in Tasks 4 and 5.
Possible Answers
- Answers will vary.
- Possible answer: Lake Ontario is lower than Lake Erie because it has a lower surface elevation. Therefore, the water would flow down from Lake Erie into Lake Ontario.
Work Time
Lake Ontario
Look at the Exploring the Great Lakes interactive again.
- Why do you think Lake Ontario is positioned lower in the diagram than the other lakes?
- What do you think happens when water flows from Lake Erie to Lake Ontario?
Drop in Depth
Lesson Guide
Continue as in Tasks 4, 5, and 6.
Possible Answers
- Students will watch the Niagara Falls video and observe how the water flows from Lake Erie to Lake Ontario.
- Niagara Falls and the Welland Canal are between Lake Erie and Lake Ontario.
Work Time
Drop in Depth
Discuss the following question from the previous task:
What do you think happens when water flows from Lake Erie to Lake Ontario?
- Watch the Niagara Falls video.
- What do you think is between Lake Erie and Lake Ontario?
VIDEO: Niagara Falls
Prepare a Presentation
Preparing for Ways of Thinking
As pairs work, identify students who:
- Organize the information and have clear explanations.
- Can clearly explain what the diagram in the interactive shows.
- Have gotten stuck at some point when they are solving one of the problems.
- Complete the Challenge Problem
Challenge Problem
Answer
- Answers will vary. Deeper exploration of the Lakes' volumes and surface areas are a good way for students to include mathematics in their answers.
For example, the combined surface areas of the four smaller lakes is about 197% the size of Lake Superior's surface area (62,450 sq mi3 1,700 sq mi = 1.97), but when using the estimated volumes calculated in the lesson, we can see that their combined volume is only about 89% of Lake Superior's volume (2,568 mi3 2,900 mi3 = .8855)
Students may also want to explore the large difference between the average depth and the maximum depth of the lakes. For example, Lake Huron's average depth is only 26% of its maximum depth. If it's volume was calculated with the maximum depth, the answer would be nearly four times as large!
Work Time
Prepare a Presentation
- Summarize what you have learned about the Great Lakes. Use your work as evidence in your summary.
Challenge Problem
- Write a paper in which you use mathematics to answer the question: “What is so great about the Great Lakes?”
Make Connections
Task 9: Make Connections
Mathematics
Have different students share their strategies and ways of approaching the problems. Encourage classmates to critique students' work and strategies.
Ask guiding questions, for example:
- How did you approach the problems? What strategies did you use?
- Why should you use average depth when calculating the volume of each lake instead of the maximum depth or surface elevation?
- Are your answers exact or an estimate? Why?
- What unit conversions were necessary to solve this problem? How did you perform these conversions?
- Why do you think the Great Lakes are great?
- How did you analyze the diagram in the interactive to find the important information?
- How can you use the different views on the diagram in the interactive to ensure your answer is reasonable?
- What are some common mistakes that could be made when solving problems like this?
- How did you persevere in finding the solution?
- How do you know that your answer is reasonable?
- What tools did you use to help you find your solution?
- What was the most challenging aspect of the problems? How did you overcome this challenge?
- Are there multiple solutions to the problems? Why or why not?
Be sure to point out that the volumes students found are estimates instead of exact answers because they used the average depth of the lakes. Since the depth of the lakes is not consistent throughout, the average depth is a close marker for the depth of the lakes, but it is still an estimate.
Emphasize the importance of unit conversions from feet to miles or square miles to square feet when calculating the volume of each lake.
Point out any mathematical processes you observed during the work period.
ELL: Give students plenty of wait time as some of your students are learning and processing mathematical information for a real world situation in a second language. Refer to the guiding questions in written form when students are presenting. Write on a chart the key points that students make during their presentations.
Performance Task
Ways of Thinking: Make Connections
- Take notes about other classmates’ approaches to finding the volume of water in the Great Lakes and their use of the problem-solving process.
As your classmates present, ask questions such as:
- How did you use the diagram in the interactive to calculate the volume of water in each lake?
- What unit conversions were necessary when calculating the volume of water in the lakes? Why?
- How can you use the graphic to make sure your answer is reasonable?
- Why should you use average depth when calculating the volume of water in each lake rather than maximum depth or surface elevation?
- Which steps of the problem-solving process were the most helpful when answering the questions?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what strategies students used to solve a problem in this lesson.
Work Time
Reflect on Your Work
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One strategy that I used to solve a problem in this lesson is…
