Students compare periodic and continuous compounding and apply continuous compounding to a variety of problem situations.

Students will use the factored forms of polynomials to find zeros of a function.
Students will use the factored forms of polynomials to sketch the components of graphs between zeros.

Students graph polynomial functions and describe end behavior based upon the degree of the polynomial.

Students transition between verbal, numerical, algebraic, and graphical thinking in analyzing applied polynomial problems.

Students transition between verbal, numerical, algebraic, and graphical thinking in analyzing applied polynomial problems.

Students model a cross-section of a riverbed with a polynomial function and estimate fluid flow with their algebraic model.

Students observe identities from graphs of sine and cosine basic trigonometric identities and relate those identities to periodicity, even and odd properties, intercepts, end behavior, and the fact that cosine is a horizontal translation of sine.

Students graph the sine and cosine functions and analyze the shape of these curves.
For the sine and cosine functions, students sketch graphs showing key features, which include intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maxima and minima; symmetries; end behavior; and periodicity.

Students formalize the periodicity, frequency, phase shift, midline, and amplitude of a general sinusoidal function by understanding how the parameters A, w, h, and k in the formula
f(x) = Asin(w(x-h))+k

are used to transform the graph of the sine function, and how variations in these constants change the shape and position of the graph of the sine function.

Students learn the relationship among the constant A, w, h, and k in the formula f(x) = Asin(w(x-h))+k
and the properties of the sine graph.

Students review how changing the parameters A, ω, h, and k in f(x) = A sin(ω(x - h)) + k affects the graph of the sine function.
Students examine the example of the Ferris wheel, using height, distance from the ground, period, and so on, to write a function of the height of the passenger cars in terms of the sine function: f(x) = A sin(ω(x - h)) + k.

Students graph the tangent function.
Students use the unit circle to express the values of the tangent function for π - x, π + x, and 2π - x in terms of tan(x), where x is any real number in the domain of the tangent function.

Students interpret addition and multiplication of two irrational numbers in the context of logarithms and find better-and-better decimal approximations of the sum and product, respectively.
Students work with and interpret logarithms with irrational values in preparation for graphing logarithmic functions.

Students compare the graph of an exponential function to the graph of its corresponding logarithmic function.
Students note the geometric relationship between the graph of an exponential function and the graph of its corresponding logarithmic function.

Students study transformations of the graphs of logarithmic functions.
Students use the properties of logarithms and exponents to produce equivalent forms of exponential and logarithmic expressions. In particular, they notice that different types of transformations can produce the same graph due to these properties.

Students understand that the change of base property allows us to write every logarithm function as a vertical scaling of a natural logarithm function.
Students graph the natural logarithm function and understand its relationship to other base b logarithm functions. They apply transformations to sketch the graph of natural logarithm functions by hand.

Students use geometric series to calculate how much money should be saved each month to have 1 million in assets within a specified amount of time.

In this Khan Academy activity, students will be given an equation and determine the amplitude of the sinusoidal function.

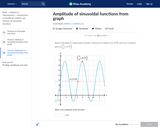
In this Khan Academy activity, students will be given a graph and determine the amplitude of the sinusoidal function.

In this task, rational functions are formally defined and connected to rational numbers. Students will use these connections to reduce rational functions and to identify rational functions that are improper and write them in an equivalent form. Students will graph rational functions that can be reduced, seeing that the graph is equivalent to the reduced function except that there is a hole in the graph, produced by the factor that is reduced. They will also graph improper rational functions and identify the slant asymptote.