- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Downloadable docs, Text/HTML
Maple Syrup
Using Ratio Tables to Solve Problems

Overview
Students focus on interpreting, creating, and using ratio tables to solve problems.
Key Concepts
A ratio table shows pairs of corresponding values, with an equivalent ratio between each pair. Ratio tables have both an additive and a multiplicative structure:
Goals and Learning Objectives
- Complete ratio tables.
- Use ratio tables to solve problems.
Introduction to Ratio Tables
Lesson Guide
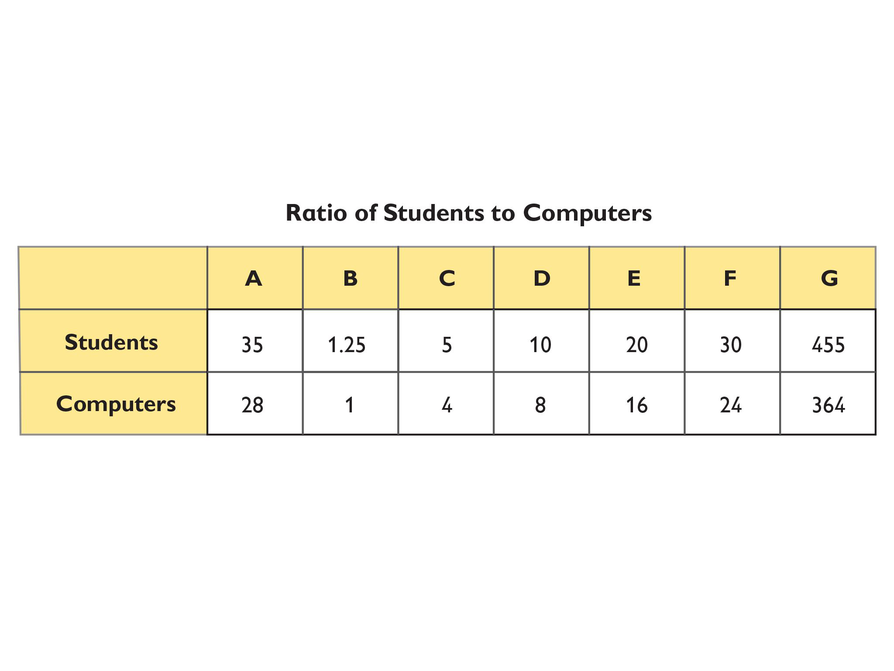
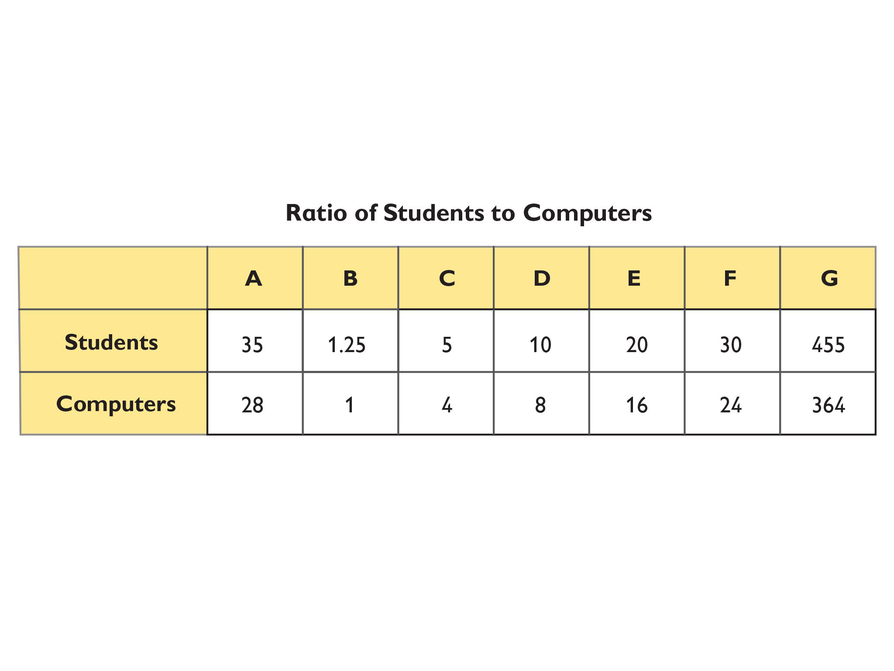
Examine the ratio table with students, explaining what each column shows.
Ask:
- Why do you think the table is called a ratio table?
ELL: Help students differentiate between comparing “within” pairs of values and “between” pairs of values. This is fundamental to conceptually understanding ratio tables. Provide students with plenty of time to make the distinction between terms and to internalize the new mathematical information.
Opening
Introduction to Ratio Tables
Discuss:
- This ratio table shows the relationship between the number of students and the number of computers in a class that has 35 students and 28 computers.
- Column A shows the ratio of students to computers, which is 35:28.
- Column B shows that there are 1.25 students for every 1 computer.
- Column C shows that the simplest whole-number ratio is 5:4.
- Columns D through G show other ways to express the ratio of students to computers using whole numbers.
More About Ratio Tables
Lesson Guide
Work through the problems with students and then answer the question as a class. If the class size grew to 40 students, then you would need 32 computers to maintain the same ratio.
SWD: Help students break down the problems into smaller parts and assist them in identifying relevant information.
Mathematics
It is important that students understand the multiplicative nature of equivalent ratios. Explain that as one quantity changes or varies, the other quantity must change or vary in a similar way in order to maintain the same relationship between the quantities. To maintain the same relationship, you can multiply or divide both quantities in a ratio by the same number.
Opening
More About Ratio Tables
If you multiply both quantities in a ratio by the same number, the resulting ratio will be equivalent to the original ratio. The calculations that follow illustrate how you can use this method to generate the ratio in column G by starting with the ratios in columns B or C.
Notice that the numbers in the ratio table are not arranged in order of size. The values in ratio tables in general do not have to follow any particular order.
- If the ratio of students to computers stays the same, how many computers would be needed if the class size grew to 40 students?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will use ratio tables to solve ratio problems.
Opening
Use ratio tables to solve ratio problems.
Fruit Punch
Lesson Guide
Have students work in pairs on the fruit punch problem.
SWD: Have students who easily understand the task demonstrate the patterns they observed to struggling students. This promotes cooperative learning and is beneficial to both the stronger student and the student who is struggling to learn the concept.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Students use a ratio table to represent the relationship between quantities in the ratio and to solve problems.
Interventions
Student looks for relationship between values within a row.
- What do you notice about the relationship between values in each column?
- Focus on the ratio between values in each column, and then compare this ratio across the columns.
- Are the ratios between the two values in each column equivalent?
Student adds the same value to each quantity instead of multiplying (or dividing) the same value.
- Is this ratio equivalent to this ratio? Explain how you know.
- Can you use another model to check that these two ratios are equivalent?
- Try multiplying both quantities in the ratio by the same number to find an equivalent ratio.
Answers
- Solutions will vary. Possible solution: 16 + 64 = 80 cups of club soda; 24 + 96 = 120 cups of grape juice; If Carlos uses 80 cups of club soda, he will need 120 cups of grape juice.
Work Time
Fruit Punch
Carlos makes his own fruit punch using grape juice and club soda to serve at his parties. He makes different amounts of punch depending on the size of the party. He has found that using the ratio 2:3 for cups of club soda to cups of grape juice makes the tastiest fruit punch.
- Complete the ratio table.
- Use the table to determine how many cups of grape juice Carlos will need if he uses 80 cups of club soda. HANDOUT: Fruit Punch
How can you use the ratio 2 : 3 and the information in the ratio table to find an equivalent ratio that will enable you to determine the amount of punch needed for 80 cups of club soda?
Maple Syrup
Lesson Guide
Have students work in pairs on the maple syrup problem.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Students use a ratio table to represent the relationship between quantities in the ratio and to solve problems.
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students need to understand the problem situation in order to set up the ratio table correctly. Look for students who may struggle, yet persevere, in finding a solution to the maple syrup problem.
Interventions
Student looks for the relationship between values within a row.
- What do you notice about the relationship between values in each column?
- Focus on the ratio between values in each column, and then compare this ratio across the columns.
- Are the ratios between the two values in each column equivalent?
Student adds the same value to each quantity instead of multiplying (or dividing) the same value.
- Is this ratio equivalent to this ratio? Explain how you know.
- Can you use another model to check that these two ratios are equivalent?
- Try multiplying both quantities in the ratio by the same number to find an equivalent ratio.
Possible Answers
Tables and solution methods will vary. Possible table and solution:
- The farmer would need 312 maple trees to get 144 gallons of maple syrup. 120 + 24 = 144 gallons of syrup; 260 + 52 = 312 trees
- Answers will vary.
Work Time
Maple Syrup
A maple tree farmer can get 30 gallons of maple syrup from 65 maple trees.
Make a ratio table to help you solve this problem. The table should show the ratio of the number of trees to the number of gallons of maple syrup for various numbers of trees.
- How many maple trees would the farmer need to get 144 gallons of maple syrup?
- How many gallons of maple syrup can he get from other numbers of maple trees?
Ask yourself:
- What ratio should you start with when making your ratio table?
- How can you get from 30 gallons of maple syrup to 144 gallons of maple syrup?
HANDOUT: Maple Syrup
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for the following student work to highlight during the Ways of Thinking discussion:
- Students who find the ratios in the table by multiplying (or dividing) both quantities in the ratio by the same value
- Students who use skip counting or repeated addition to fill in the missing numbers in the table
- Students who notice relationships between ratios to find other ratios.
Challenge Problem
Possible Answers
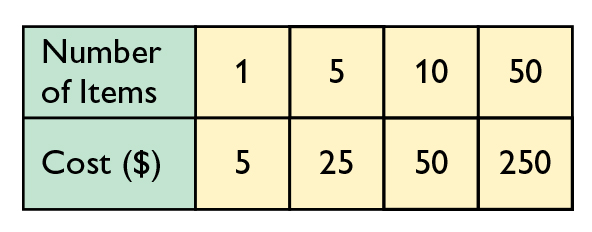
- Answers will vary. Possible answers: If you know the cost of one item, you could use a ratio table to find a predicted cost for x items. Then you could compare the offered price of x items to the predicted cost of x items. For example, if one item cost $5, it has a ratio of 1:5. You could set up a ratio table to find the cost for 50 items.
The equivalent ratio would be 50:250, with a cost of $250. You would know you are getting a good deal if the store offered the 50 items for a price lower than $250. Or: No, a ratio table would not be useful for finding the price of discounted quantities. If you use the unit price to find the price of the larger quantity, the price will not reflect the discount the store is offering.
Work Time
Prepare a Presentation
Present your ratio table.
- Explain the strategy you used for constructing a ratio table that helps you solve the problem of determing how many trees would be needed to make 144 gallons of maple syrup.
- Explain how you put other pairs of numbers representing equivalent ratios into the table.
Challenge Problem
Would using a ratio table help you solve problems about calculating the costs of items in a store if the store offered special deals for buying large quantities of an item? Explain.
Make Connections
Mathematics
Begin the discussion with presentations of at least two different ways to use the ratio table to solve the maple syrup problem. If no one addresses it, invite students to think about what can be added together in the table in order to solve the problem.
Sample methods:
Method 1
Double 72 gallons equals 144 gallons of maple syrup, so double 156 trees would be 312 trees.
Method 2
1 ⋅ 144 = 144
Method 3
144 ÷ 6 = 24
13 ⋅ 24 = 312
Close the discussion with a presentation from at least one pair of students who attempted the Challenge Problem.
SWD: One way to start the discussion is to ask students what questions arose during the maple syrup problem. Student-initiated inquiry promotes connection and engagement with the mathematics. Provide positive feedback, using gestures and prompting, to elicit deeper responses.
ELL: During class discussions, make sure you provide wait time for ELLs (5–10 seconds) and acknowledge student responses, both verbally and with gestures.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
As students make their presentations, encourage other students to ask questions and critique the solution method. Presenters will need to articulate their reasoning in response.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates' strategies for using ratio tables to solve ratio problems.
As your classmates present, ask questions such as:
- What were some of the challenges you encountered in making your ratio table?
- What does your ratio table show?
What I Learned about Ratio Tables
A Possible Summary
Ratio tables show equivalent ratios between two quantities. You can create a ratio table by multiplying (or dividing) both quantities in the ratio by the same value to find an equivalent ratio. A ratio table can help you find equivalent ratios in order to solve problems.
Formative Assessment
Summary of the Math: What I Learned about Ratio Tables
Write a summary about making and using ratio tables.
Check your summary.
- Do you explain what a ratio table is?
- Do you explain how to make a ratio table?
- Do you describe how you can use a ratio table to solve ratio problems?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out how students think a ratio table is similar to or different from a double number line.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starters below if you find them to be helpful.
I think a ratio table is similar to a double number line because …
I think a ratio table is different from a double number line because …