- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Number Line Tool
Ratio Table Tool
Ratio Table Tool
Student Self Check

Overview
Students begin the lesson with a critique of their own work on the Self Check using questions and comments from you to reflect on their work. They then critique three examples of student work on the task, each with its own tools for modeling the given relationship between quantities. Finally, they apply what they learned to a closely related problem.
Key Concepts
Students reflect on their work and connect different ways of representing ratio relationships: tape diagrams, double number lines, and ratio tables.
Goals and Learning Objectives
- Use teacher comments to refine solution strategies for ratio problems.
- Deepen understanding of ratio relationships.
- Synthesize and connect strategies for representing and investigating ratio relationships.
- Critique given student models created to solve ratio problems.
- Apply deepened understanding of ratio relationships to a new ratio problem.
Critique
Lesson Guide
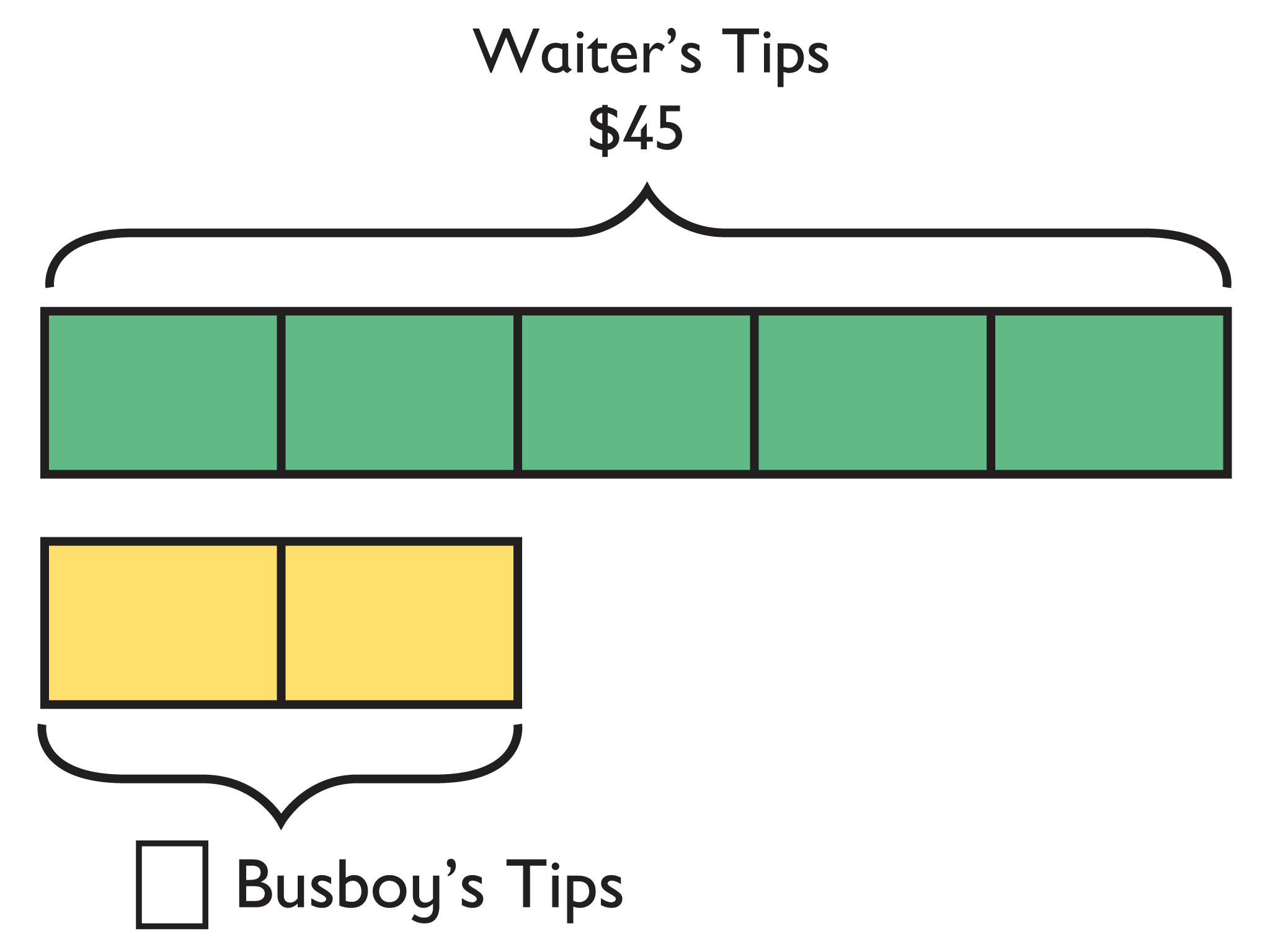
Return students’ solutions to the Self Check task and ask them to think about the following questions.
- Did you identify the quantities in the situation, both known and unknown, and then use a tool to represent how the quantities are related?
- Did you make a conjecture about the amount the waiter gave the busboy? Is this amount less than or greater than $45?
- How can you demonstrate that your answer is correct?
SWD: Post the Interventions in the classroom for students to use as a resource as they work. Create and provide an enhanced version of the Interventions with embedded text structures (labels, highlights, words in bold) to cue students to pay closer attention to particular terms.
ELL: In asking these prompting questions, be sure to use adequate pace with ELLs, and be sure that they understand meaning of the questions.
Opening
Critique
Revise your work on the Self Check problem from the last lesson, based on the following questions.
- Did you identify the quantities in the situation, both known and unknown, and then use a tool to represent how the quantities are related?
- Did you make a conjecture about the amount the waiter gave the busboy? Is this amount less than or greater than $45?
- How can you demonstrate that your answer is correct?
INTERACTIVE: Double Number Line Tool
INTERACTIVE: Ratio Table Tool
Math Mission
Lesson Guide
Discuss the Math Mission. Students will revise their work on the Self Check task based on feedback, correct other students’ solutions to the problem, and solve a similar problem.
Opening
Revise your work, correct other students’ solutions, and solve a similar problem.
Chen’s Work
Lesson Guide
Have students work in pairs to critique Chen’s solution.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
After three exercises of critique, along with reflections on their own work on the Self Check task, students are directly set up to solve the related problem having just considered an analogous problem. They have multiple conceptual and visual tools to draw on, and they should show perseverance in the face of any difficulty they have in interpreting, representing, and solving the problem.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
In critiquing the given sample student solutions to the Self Check task, students must understand another person’s reasoning, recognize and analyze errors in the work, and articulate ways of improving the work.
Mathematical Practice 5: Use appropriate tools strategically.
Students are invited to reflect on the usefulness, and correct use, of tape diagrams, double number lines, and ratio tables. They should understand these as tools they can choose to use as they see fit for modeling ratio relationships between quantities.
Mathematical Practice 6: Attend to precision.
At least two of the errors made in the given solutions can be considered examples of imprecision: incorrectly identifying the elements of the tape diagram that represent quantities in the situation and incorrectly aligning the double number line. These errors highlight the importance of constructing mathematical representations with careful attention to detail and accuracy.
Interventions
Student has difficulty interpreting and/or using a particular model for representing a ratio relationship.
- Tape diagram: How much is each unit of your tape diagram worth?
- Tape diagram: Whose tape should be longer, the busboy’s or the waiter’s?
Possible Answers
The tape diagram shows a ratio of 5:2, with the 5 units in the upper tape representing the waiter’s $45 and the 2 units in the lower tape representing the busboy’s unknown amount.
If the upper tape represents $45, then each unit represents $9, and the busboy’s amount is 2 ⋅ $9 = $18.
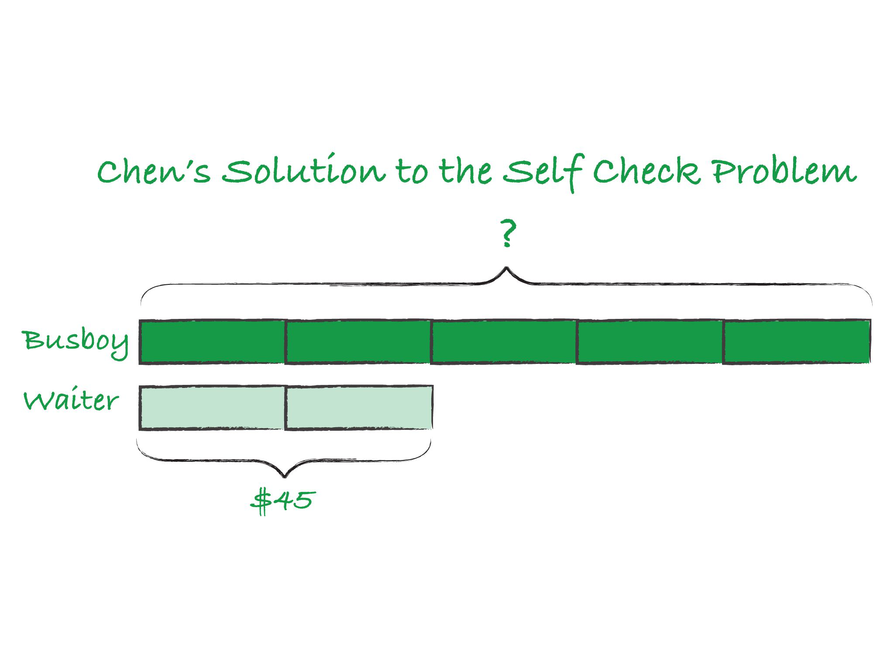
- Chen reversed the busboy and the waiter in the tape diagram from the way it should be.
- Chen could have used the top tape to represent the waiter’s tips ($45), and then each unit of tape would be $9. Then he could use the bottom tape to represent the busboy’s tips, with two units equaling $18.
Work Time
Chen's Work
The problem:
A waiter at a restaurant shares his tips with the busboy in a ratio of 5:2. If the waiter had $45 after sharing his tips, how much did he give the busboy?
Chen says:
“My tape diagram shows that 2 units are equal to the waiter’s $45, because the ratio is 5:2. So each unit represents half of $45, or $22.50. The busboy is represented by 5 units. And $22.50 × 5 is $112.50. So the waiter gave the busboy $112.50.”
- What mistake did Chen make?
- Is there a way he could have used a tape diagram to solve the problem correctly? Explain.
Carlos’s Work
Lesson Guide
Have students work in pairs to critique Carlos’s solution.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
After three exercises of critique, along with reflections on their own work on the Self Check task, students are directly set up to solve the related problem having just considered an analogous problem. They have multiple conceptual and visual tools to draw on, and they should show perseverance in the face of any difficulty they have in interpreting, representing, and solving the problem.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
In critiquing the given sample student solutions to the Self Check task, students must understand another person’s reasoning, recognize and analyze errors in the work, and articulate ways of improving the work.
Mathematical Practice 5: Use appropriate tools strategically.
Students are invited to reflect on the usefulness, and correct use, of tape diagrams, double number lines, and ratio tables. They should understand these as tools they can choose to use as they see fit for modeling ratio relationships between quantities.
Mathematical Practice 6: Attend to precision.
At least two of the errors made in the given solutions can be considered examples of imprecision: incorrectly identifying the elements of the tape diagram that represent quantities in the situation and incorrectly aligning the double number line. These errors highlight the importance of constructing mathematical representations with careful attention to detail and accuracy.
Interventions
Student has difficulty interpreting and/or using a particular model for representing a ratio relationship.
- Double number line: Does your double number line show correspondence between $5 for the waiter and $2 for the busboy? What other pairs of values correspond?
- Double number line: Are the zeros on your two number lines lined up?
Possible Answers
- Carlos did not correctly line up the busboy number line with the waiter number line.
- Carlos should have been more careful about labeling the units on the bottom number line showing the busboy’s tips. Each unit length on the busboy’s number line should have a value of 2 and should correspond directly with each unit length on the waiter’s number line with a value of 5. This way, 5 on the waiter number line would line up with 2 on the busboy number line, 10 would line up with 4, and so on, and 45 would line up with 18.
Work Time
Carlos's Work
The problem:
A waiter at a restaurant shares his tips with the busboy in a ratio of 5:2. If the waiter had $45 after sharing his tips, how much did he give the busboy?
Carlos says:
“I used a double number line. First I made a number line for the waiter that went from 0 to 65, counting by 5s. Then I made a number line for the busboy. I lined up $5 for the waiter with $1 for the busboy. Then I could see what lined up with $45 for the waiter. Since $9 lines up with $45 for the waiter, the waiter gave the busboy $9.”
- What mistake did Carlos make?
- Is there a way he could have used a double number line to solve the problem correctly? Explain.
Jan’s Work
Lesson Guide
Have students work in pairs to critique Jan’s solution.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
After three exercises of critique, along with reflections on their own work on the Self Check task, students are directly set up to solve the related problem having just considered an analogous problem. They have multiple conceptual and visual tools to draw on, and they should show perseverance in the face of any difficulty they have in interpreting, representing, and solving the problem.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
In critiquing the given sample student solutions to the Self Check task, students must understand another person’s reasoning, recognize and analyze errors in the work, and articulate ways of improving the work.
Mathematical Practice 5: Use Appropriate tools strategically.
Students are invited to reflect on the usefulness, and correct use, of tape diagrams, double number lines, and ratio tables. They should understand these as tools they can choose to use as they see fit for modeling ratio relationships between quantities.
Mathematical Practice 6: Attend to precision.
At least two of the errors made in the given solutions can be considered examples of imprecision: incorrectly identifying the elements of the tape diagram that represent quantities in the situation and incorrectly aligning the double number line. These errors highlight the importance of constructing mathematical representations with careful attention to detail and accuracy.
Interventions
Student has difficulty interpreting and/or using a particular model for representing a ratio relationship.
- Ratio table: Does each pair of values in your table have a ratio equivalent to 5:2?
- Ratio table: What are some other possible pairs of values you could enter in your table, if you didn’t know the waiter’s tip amount?
Possible Answers
- Jan added rather than multiplied to get the next column’s entries in the ratio table.
- Jan should multiply both values by the same number to get an equivalent ratio. Each pair of corresponding values should have a ratio equivalent to 5:2, so multiplying 5 and 2 each by 9 would give the correct ratio for the waiter’s $45 in tips: 45 to 18.
Work Time
Jan's Work
The problem:
A waiter at a restaurant shares his tips with the busboy in a ratio of 5:2. If the waiter had $45 after sharing his tips, how much did he give the busboy?
Jan says:
“I set up a ratio table. I knew when the waiter got $5, the busboy got $2, because the ratio was 5 to 2. So I put that in the table. Then I wanted to see what would happen when the waiter got $45, so I added $40 to $5 and put it in the table for the waiter. I wanted to do the same thing for the busboy, so I added $40 to $2 and got $42 to match up with the $45 for the waiter. So when the waiter gets $45, the busboy gets $42.”
- What mistake did Jan make?
- Is there a way she could have used a ratio table to solve the problem correctly? Explain.
Revise Your Work
Lesson Guide
Have students work in pairs to revise their work.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
After three exercises of critique, along with reflections on their own work on the Self Check task, students are directly set up to solve the related problem having just considered an analogous problem. They have multiple conceptual and visual tools to draw on, and they should show perseverance in the face of any difficulty they have in interpreting, representing, and solving the problem.
Interventions
Student has difficulty interpreting the situation.
- Who makes more in tips, the waiter or the busboy?
- Draw a picture to represent how the tips are shared, and label it accurately. Can you represent the same information with a tape diagram?
Student makes a mistake similar to one made in one of the three given solutions.
- Think back to [Chen’s/Carlos’s/Jan’s] work. What mistake did the student make?
- Check that your model is as precise and accurate as possible so that you aren’t making a mistake like Chen, Carlos, or Jan.
Possible Answers
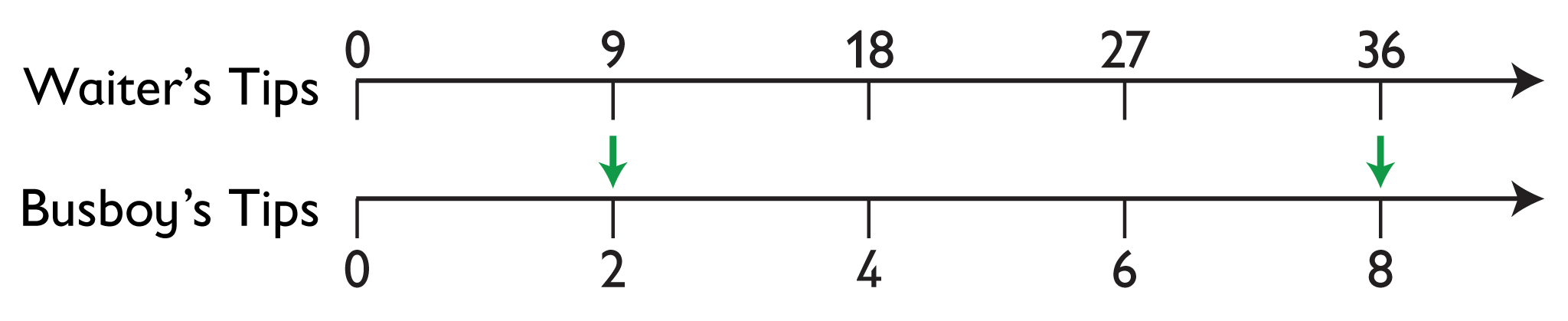
- The waiter gave the busboy $8. Using a double number line to show a ratio of 9:2, the 9 on the number line representing the waiter’s tips corresponds with the 2 on the number line representing the busboy’s tips. The double number line shows that the value corresponding with $36 (4 units of $9 each) is $8 (4 units of $2 each).
Work Time
Revise Your Work
Working with a partner, use what you learned from correcting student work to solve this problem.
- A waiter shares his tips with the busboy in a ratio of 9:2. If the waiter had $36 after sharing his tips, how much did he give the busboy?
INTERACTIVE: Double Number Line Tool
INTERACTIVE: Ratio Table Tool
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for the following student thinking to highlight during the Ways of Thinking discussion:
- Students who refer to their work on the Self Check task and to your comments and questions about that work
- Students who reflect on the mistakes made in the three given approaches to the Self Check task in thinking about the Work Time problem
Work Time
Prepare a Presentation
Explain how you revised your work. Support your explanation using both your work on the Self Check and your new work.
Make Connections
Lesson Guide
Have students share different models for the new waiter problem, and have them critique or suggest ways of refining one another’s work.
Mathematics
If most students have correct answers and complete and correct models, invite students to make explicit connections between types of models to deepen their understanding of each type of representation. Ask:
- How is the ratio shown in the tape diagram? (Answer: as a comparison between lengths)
- How is the ratio shown on the double number line? (Answer: as pairs of values that line up, each with an equivalent ratio)
- How is the ratio shown in the ratio table? (Answer: as pairs of values in each column, each with an equivalent ratio)
- In the tape diagram, each unit of length represents the same value. Is this true on the double number line? (Answer: No, each unit of length on one number line represents a different value from each unit of length on the other number line. The value represented by these units is determined by the ratio. In a tape diagram, the length of each whole tape is determined by the ratio.)
- Are there units in the ratio table? (Answer: If a dollar is considered a unit, then each value in the waiter’s row increases by 9 units with each increase in the busboy’s value of 2 units. If you wanted to show single unit increases between columns, you could show that each single dollar increase in the busboy’s tips corresponds to an increase of $4.50 in the waiter’s tips.)
- What do the ratio table and double number line show that the tape diagram doesn’t? (Answer: They show multiple possible values for each quantity that have an equivalent ratio, rather than just one case. On the other hand, by changing the total value represented by either tape in a tape diagram or by changing the value represented by each unit, you can show multiple cases that satisfy the constraint given by the ratio.)
ELL: Provide ELLs and other students a sample or model for the concepts, strategies, and applications that will be addressed in the Assessment, as well as the format you want them to follow. Be prepared to address and explicitly re-teach or review vocabulary, concepts, strategies, and applications.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates' suggestions for correcting the student work and their approaches to solving the new waiter problem.
As your classmates present, ask questions such as:
- Did correcting the student work help you solve the new waiter problem? How?
- How does your tool show the ratio between the amount the waiter keeps and the amount he gives to the busboy?
- Can you identify a unit in a tape diagram, on a double number line, and in a ratio table?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out what students learned in this unit.
SWD: Some students may struggle to initiate writing for this reflection. Prompt them to refer to the sentence starter as a support. Provide students with scaffolding questions about the ideas that were discussed in class or a bulleted list of ideas that were discussed about which the students can write. In addition to the sentence starter, students may also benefit from paragraph frames such as:
- “So far, I have completed … .”
- “I have noticed that … .”
- “The parts I found challenging were … .”
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One of the most important things I learned in this unit is …