- Author:
- Pearson
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Self Check Review

Overview
Students work in pairs to critique and improve their work on the Self Check from the previous lesson.
Key Concepts
To critique and improve the task from the Self Check and to complete a similar task with a partner, students use what they know about solving equations and relating the equations to real-world situations.
Goals and Learning Objectives
- Solve equations using the addition or multiplication property of equality.
- Write word problems that match algebraic equations.
- Write equations to represent a mathematical situation.
Critique
Lesson Guide
Students should look at the results of their Self Check task and review the questions.
Opening
Critique
Review your work on the Self Check problem and think about the following questions.
- What can you do to both sides of the equation to get x by itself on one side?
- What property of equality can you use to solve the equation?
- Substitute your solution back into the original equation. Do you get a true equation?
- Can you think of a real-world situation about the height of something, the cost of something, or earning money?
- Can you think of a proportional situation for the last equation?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will show what they know about solving equations and interpreting what the equations mean.
Opening
Show what you know about solving equations and interpreting what they mean.
Revise and Extend Your Work
Lesson Guide
Have students work in pairs to revise their work from the Self Check. Encourage students to incorporate ideas from their partner in their revisions. Then students will work together on a similar task.
While students work with their partners, note different approaches to the task:
- How do they organize their work?
- Do they notice if they have chosen a strategy that does not seem to be productive? If so, what do they do?
Support student problem solving:
- Try not to make suggestions that move students to a particular approach. Instead ask questions that help students clarify their thinking.
- If students find it difficult to get started, these questions might be helpful:
- What feedback questions were you asked?
- How could you and your partner work together to address one or more of those feedback questions?
If several students in the class are struggling with the same issue, you could write a relevant question on the board. You might ask a student who has performed well on a particular part of the task to help a struggling student.
If students are struggling with the new task, have them begin by reviewing the corresponding part of the previous task.
SWD: Some students with disabilities may struggle to complete all the tasks in the time allotted. Consider providing these supports:
- Reduce the number of tasks that some students need to complete during this lesson; however, be sure that these students demonstrate understanding of necessary skills.
- Partner students with disabilities with typically developing peers as support and/or assign partners different jobs to reduce the number of tasks each individual is expected to complete.
- Highlight specific areas/skills from the Interventions on which students should focus.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them
Students must make sense of the task. They must plan and carry out a solution strategy.
After they complete the task, they must go back and check that their solution makes sense. Students also have the opportunity to work with another student and try to understand his or her approach to the task.
Mathematical Practice 6: Attend to precision.
Students are asked to present their work in a clear, precise way. They should try to use correct mathematical language and symbols and to label their work carefully so it is easy to follow.
Interventions
Student solves the equation incorrectly.
- Did you use the correct property of equality?
- Did you check all your calculations?
- Did you use substitution to check your solution?
Student's word problem does not match the equation given.
- Work backwards. Read the word problem you wrote. Write an equation that represents it. Does it match the equation you were given?
Answers
- x + 5 = 17
x + 5 − 5 = 17 − 5 (Addition property of equality)
x = 12
Word problems will vary. Possible answer: A shirt costs $5 more than a pair of shorts. The shirt costs $17. How much does the pair of shorts cost? Answer: The pair of shorts costs $12.
- 4x = 22
Word problems will vary. Possible word problem: Four books cost $22. Each costs the same amount. How much does one book cost? Answer: One book costs $5.50.
Word problems will vary. Possible answer: A purple paint is mixed in the ratio of 5 parts blue to 8 parts red. How much blue paint should be mixed with 6 cups of red paint to get the same shade of purple? Answer: You should mix cups of blue paint.
Work Time
Revise and Extend Your Work
Work with your partner to revise your work on the Self Check, based on the questions from the Opening and feedback from your partner or your teacher.
Self Check
For each equation do the following.
- Solve the equation. Name the property of equality you use and show each step.
- Then write and solve a word problem that each equation could represent.
- x + 5 = 17
- 4x = 22
Solve the Equations
Lesson Guide
Have students work together on this task.
While students work with their partners, note different approaches to the task:
- How do they organize their work?
- Do they notice if they have chosen a strategy that does not seem to be productive? If so, what do they do?
Support student problem solving:
- Try not to make suggestions that move students to a particular approach. Instead ask questions that help students clarify their thinking.
- ELL: Provide ELLs and other students a sample or model for the concepts, strategies, and applications that will be addressed in the quiz, and the format you want them to follow. Be prepared to address and explicitly re-teach or review vocabulary, concepts, strategies, and applications.
Interventions
Student solves the equation incorrectly.
- Did you use the correct property of equality?
- Did you check all your calculations?
- Did you use substitution to check your solution?
Student's word problem does not match the equation given.
- Work backwards. Read the word problem you wrote. Write an equation that represents it. Does it match the equation you were given?
Neither student can think of a scenario that matches the equation.
- For 8= x + 6.5, think about 6.5 as a distance in miles.
- For , think about 8 as the length of a piece of string in inches.
- For , think about a juice mixture.
Possible Answers
Word problems will vary. Possible word problem: Mr. Brown is driving from his house to the mall. The distance is 8 miles. He has 6.5 miles left to drive. How far has he driven so far? Answer: He has driven 1.5 miles so far.
Word problems will vary. Possible word problem: A piece of string is cut in half. Each piece is 8 inches long. How long was the string before it was cut? Answer: The string was 16 inches long before it was cut.
Word problems will vary. Possible answer: An orange-pineapple juice is made with 4 parts orange juice for every 7 parts pineapple juice. How much orange juice should you mix with 5 cups of pineapple juice? Answer: You should mix cups of orange juice.
Work Time
Solve the Equations
For each equation do the following.
- Solve the equation. Show all steps and write the property you use.
- Then write a word problem that the equation could represent.
Prepare a Presentation
Prepare for Ways of Thinking
- Look for anyone who solved the equation incorrectly and use it as an example to examine what went wrong.
- Look for student work that explains the addition property of equality.
- Look for student work that explains the multiplication property of equality.
- Look for student work that justifies every step of solving the equation and checks the answer. Use this as model of grade-level work.
Challenge Problem
Answer
Work Time
Prepare a Presentation
- Explain how you use the properties of equality to solve equations.
- Support your explanations with your work.
Challenge Problem
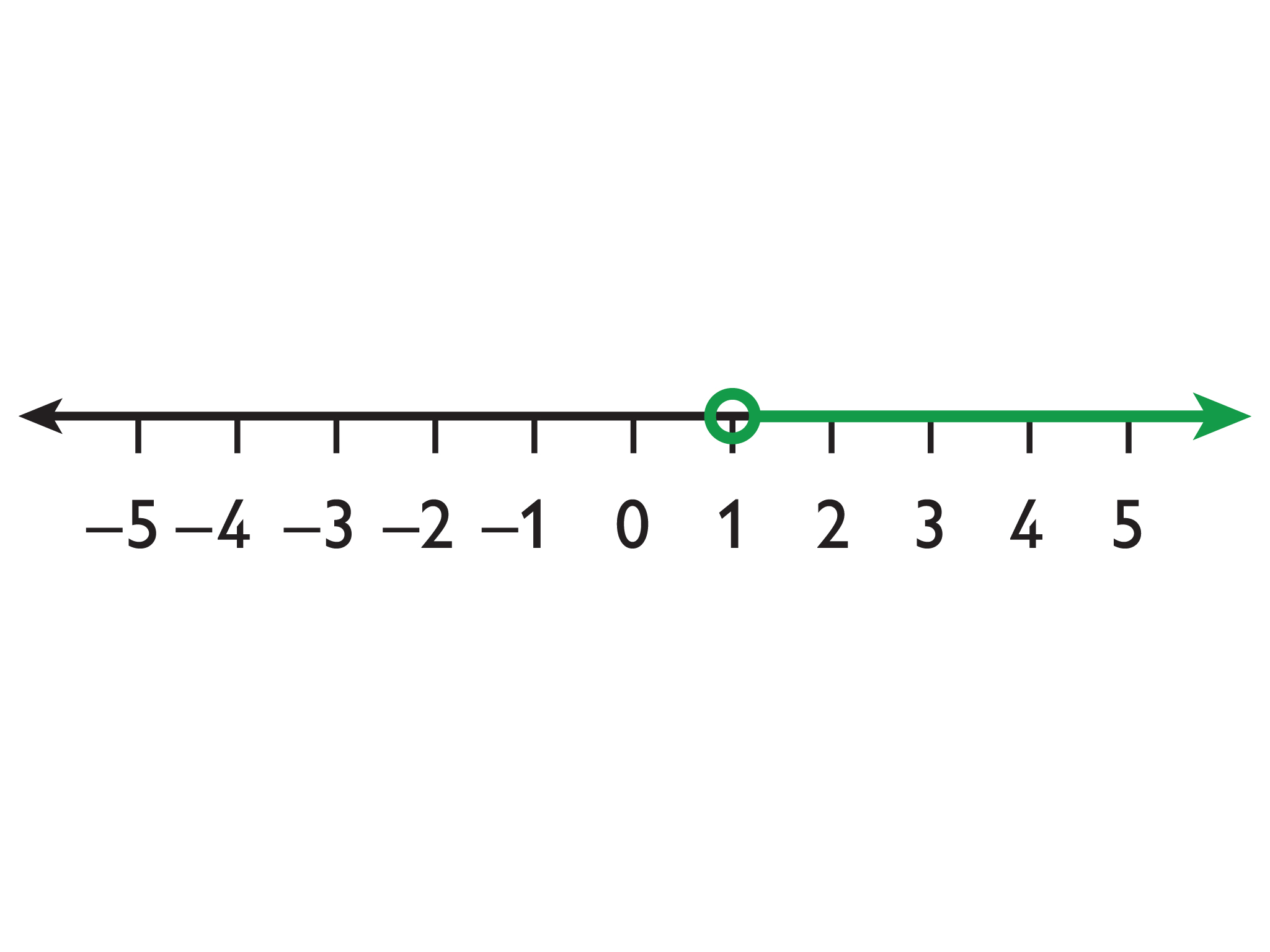
- Use the Inequality Number Line to show all possible solutions to the inequality:
3x + 7 > 10
INTERACTIVE: Representing Inequalities on a Number Line
Make Connections
Lesson Guide
Allow pairs who used different solution methods to present their work. Include students who made errors. Try to allow as many students as possible to share the word problems they have written.
Have students make observations and ask questions as different pairs present their work. Encourage students to talk about how they revised their work based on feedback.
For the Challenge Problem, students may first solve the equation 3x + 7 = 10 to get x = 1 and then decide through reasoning or through substitution that numbers greater than 1 will make the inequality true. Allow students to explain their reasoning while others ask questions. If several students present their solutions, have students tell which explanation they think was the clearest.
SWD: For students with disabilities, participating in a whole-class discussion such as Ways of Thinking can be intimidating for a variety of reasons. However, it is important for students to work on the speaking and listening skills implicit to this portion of the lesson. Possible supports for students include:
- Give students a few minutes to discuss their ideas, the questions posed, and what they learned in the lesson with a partner or small group before sharing out in the whole-class setting.
- Conference with individual students prior to the discussion to ascertain what they might be able to successfully contribute to the discussion. Give students time to rehearse their contribution.
Performance Task
Make Connections
Take notes about your classmates' approaches and the steps they used to solve each equation.
Hint:
As your classmates present, ask questions such as:
- Why didn't you add 6.5 to both sides in the problem
8 =x + 6.5? - Why did you multiply both sides of the equation by 2 in the problem 12 x = 8?
- Why did you divide when you used the multiplication property of equality?
Reflect On Your Work
Lesson Guide
Have each student write a quick reflection before the end of the class. Review the reflections to find out what more students would like to learn about equations and inequalities.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I still would like to learn about equations and inequalities is …