- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Graphing the Height of the Miniature
Proportional Relationships In Graphs

Overview
Students continue to explore the three relationships from the previous lessons: Comparing Dimensions, Driving to the Amusement Park, and Temperatures at the Amusement Park. They graph the three situations and realize that the two proportional relationships form a straight line, but the time and temperature relationship does not.
Key Concepts
A table of values that represent equivalent ratios can be graphed in the coordinate plane. The graph represents a proportional relationship in the form of a straight line that passes through the origin (0, 0). The unit rate is the slope of the line.
Goals and Learning Objectives
- Represent relationships shown in a table of values as a graph.
- Recognize that a proportional relationship is shown on a graph as a straight line that passes through the origin (0, 0).
Graphs
Lesson Guide
- Read the prompt aloud.
- Have student pairs discuss the question, “How is the relationship visible in the graph?”
Tell students that mathematicians use tools and representations to solve and understand problems; today they will create graphs strategically to better understand the problems in the previous two lessons. Let students know that this mathematical practice complements other mathematical practices (e.g., Mathematical Practice 4: Model with mathematics; and Mathematical Practice 6: Attend to precision) and that they will continue to use these mathematical practices for the rest of the school year and beyond.
Mathematics
A graph makes a relationship between quantities visible in ways that a table and formula do not. (The emphasis of the beginning of the lesson should be on this idea rather than on the mechanics of graphing or the specific features of graphs of proportional relationships.) In a formula, the quantities are represented by letters, and the relationship between them is shown by a particular combination of operations, values, and an equal sign. In a table, the quantities are each represented as a row (or column) of values, and the relationship between the values is shown as the correspondence between the pairs of values. On a graph, the quantities are shown on the axes, and the relationship between them is shown by the set of points defined by corresponding pairs of values. Ask your students the following:
- To represent a relationship between two quantities in a table, where do the quantities go? How do you see the relationship between them?
- To represent a relationship between two quantities in a formula, where do the quantities go? How do you see the relationship between them?
- To represent a relationship between two quantities on a graph, where do the quantities go? How do you see the relationship between them?
Opening
Graphs
In this lesson, you will create graphs. Mathematical representations enable mathematicians and scientists to visualize problems—and solutions to problems—in ways that help them further explore the mathematics of a situation. It also allows them to detect possible errors in their work, and to make generalizations based on specific quantities in a situation in order to gain a broader perspective on the relevant mathematics.
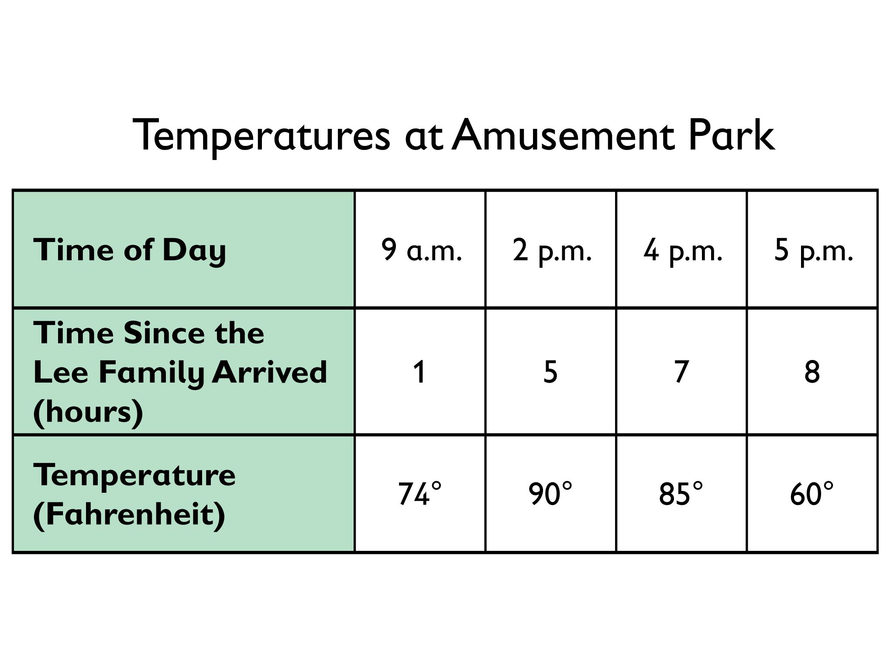
Look at the table about the temperature at the park in relationship to the time of day.
- You can make the relationship even more visible by representing it as a graph. Create a graph based on the table.
- How is the relationship visible in the graph?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will graph relationships and determine if the relationship is proportional by looking at the graph.
Opening
Graph relationships and determine if the relationship is proportional by looking at the graph.
Driving to the Park
Lesson Guide
Have students work in pairs on all problems and the presentation.
SWD: If students are demonstrating difficulty interpreting and analyzing the information in the representations of data (and the relationships between the data), highlight the columns that correlate or color-code values to show how they relate to each other on the graph. Some students may need support plotting points. Provide direct instruction for those students.
Interventions
Student understands the graph but doesn’t understand the meaning of the points or how to plot them.
- Each point on your graph shows the correspondence between two values, one for each quantity.
- Each column in the table gives you two values, one for each quantity. This pair of values is a coordinate pair, and gives you the coordinates of a single point.
Student doesn’t see the straight lines in the graphs for the first two problems.
- Would it make sense to connect the points of your graph? Think about the situation it represents.
- Are the points of your graph the only possible points in the situation, or could there be more? If you wanted to plot more points in this relationship, where would the points go on the graph?
- Connect the points and describe the graph to your partner.
SWD: Students with visual-spatial challenges may struggle to independently find patterns in the data, even if it seems straightforward. Model how to identify the pattern with the relationships given in the table. Transferring this information into a graph may be more challenging for some students, especially those who have trouble transferring information from one form to another. Give direct instruction on or guided practice with graphing skills.
ELL: When presenting these guiding questions from the Interventions section, be sure that ELLs can follow what you are saying. Provide written questions and use a pace that is appropriate for non-English speakers. Discuss new vocabulary (e.g., equivalent ratios, proportional relationships) at a slower pace to ensure understanding and recollection of meaning.
Answers
Work Time
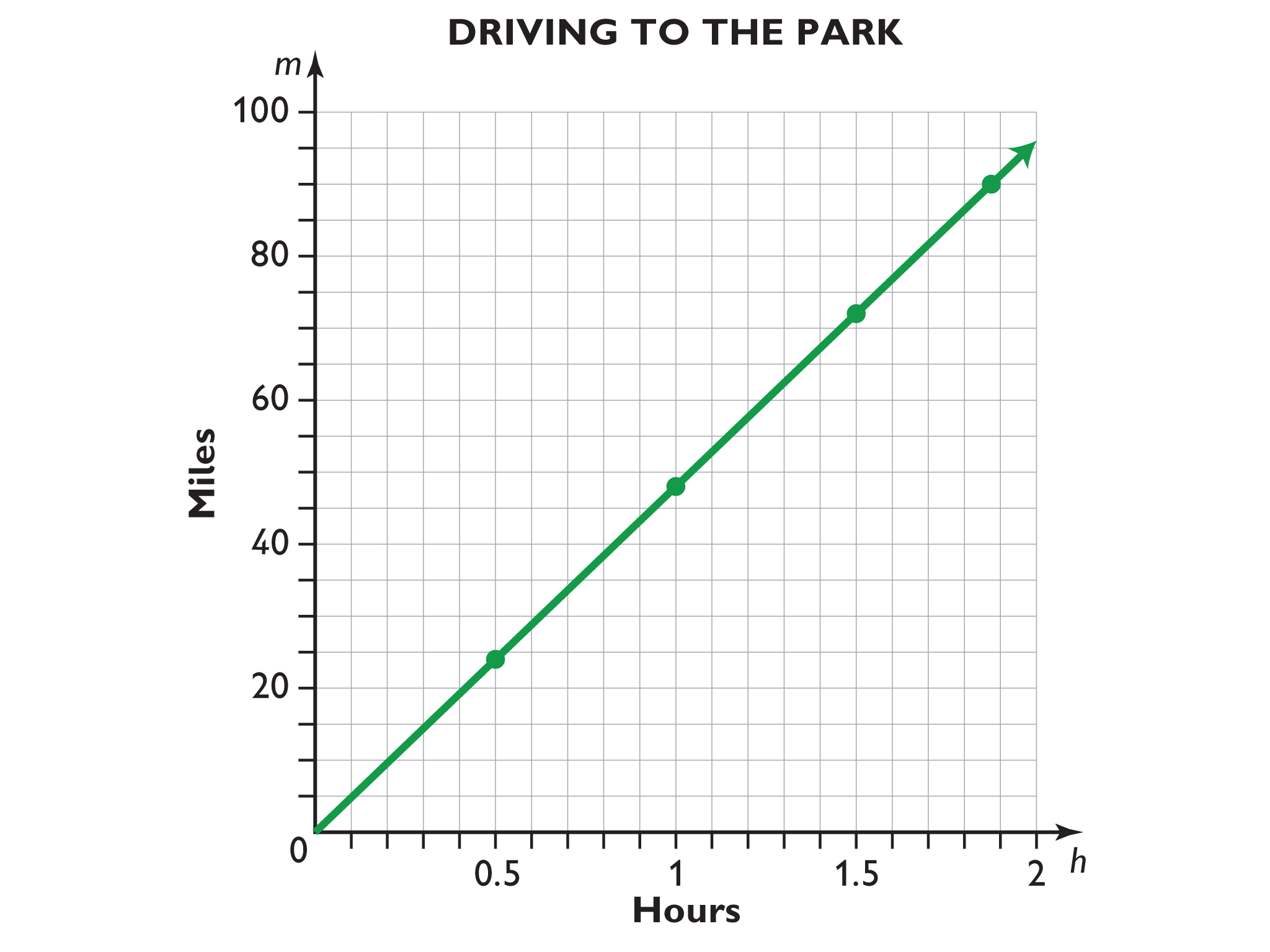
Driving to the Park
Look at the formula you created in Lesson 3 showing the relationship between the time Mr. Lee drove and the distance he traveled. Create a graph based on the table.
INTERACTIVE: Driving to the Park
Hint:
- What are the two variables in the situation?
- Which of these variables should you put on the
x -axis? What scale should you use? - Which of these variables should you put on the
y -axis? What scale should you use? - Did you plot the points or enter the formula?
- What shape was the graph?
Height of the Miniature
Interventions
Student doesn’t understand the meaning of the points or how to plot them.
- Each point on your graph shows the correspondence between two values, one for each quantity.
- Each column in the table gives you two values, one for each quantity. This pair of values is a coordinate pair, and gives you the coordinates of a single point.
Student doesn’t see the straight lines in the graphs for the first two problems.
- Would it make sense to connect the points of your graph? Think about the situation it represents.
- Are the points of your graph the only possible points in the situation, or could there be more? If you wanted to plot more points in this relationship, where would the points go on the graph?
- Connect the points and describe the graph to your partner.
Answers
Work Time
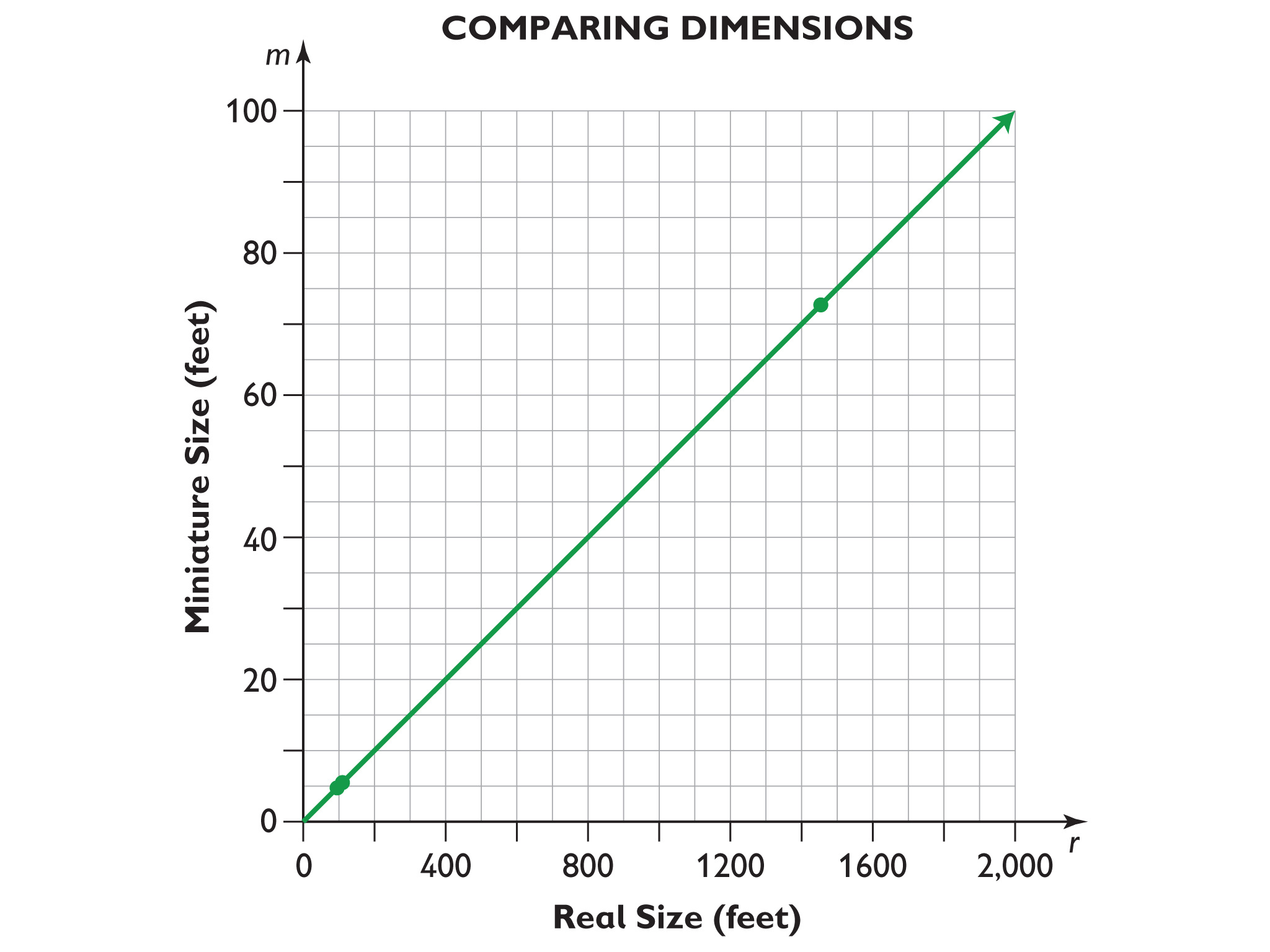
Height of the Miniature
Look at the formula you created in Lesson 3 showing the relationship between the dimensions of the real Empire State Building and the miniature building in the amusement park.
Look at the table showing the relationship between the dimensions of the real Empire State Building and the miniature building in the amusement park.
- Create a graph based on the table.
Note: You might have to scale the axes on the graph to represent the points.
INTERACTIVE: Graphing the Height of the Miniature
Hint:
- What are the two variables in the situation?
- Using a scale of 0 to 1,500 might make the graph too small. You might want to start with this scale, plot two points, and then change the scale.
Make and Compare Graphs
Answers
- The graphs for the problems about driving to the amusement park and comparing dimensions (Empire State Building) are both straight lines.
- Answers will vary. Students should mention the presence or absence of a constant ratio between pairs of corresponding values.
- You can see the constant of proportionality in the slope (or the steepness) of the line. To know the value of the constant of proportionality, you have to pay attention to the scales of the axes and the actual values that are paired together at each point.
Work Time
Make and Compare Graphs
Compare the three graphs you created in this lesson.
- How do the shapes of the graphs compare? Are any of the graphs straight lines?
- What do you think differences in shape mean? For example, if one graph is a straight line and another is not, what does this tell you?
- Where do you “see” the constant of proportionality in the Empire State Building graph and the time/distance graph?
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for students who:
- Have an exploratory attitude toward graphing
- Use the graphs to ask and answer questions about the graph and the situation
- Discuss and debate about the scale of the axes
- Discuss and debate about whether to connect the points of a graph
- Discuss and debate about whether it makes sense to put one quantity or the other on the horizontal or vertical axis and whether it changes the meaning of the graph
Challenge Problem
Answers
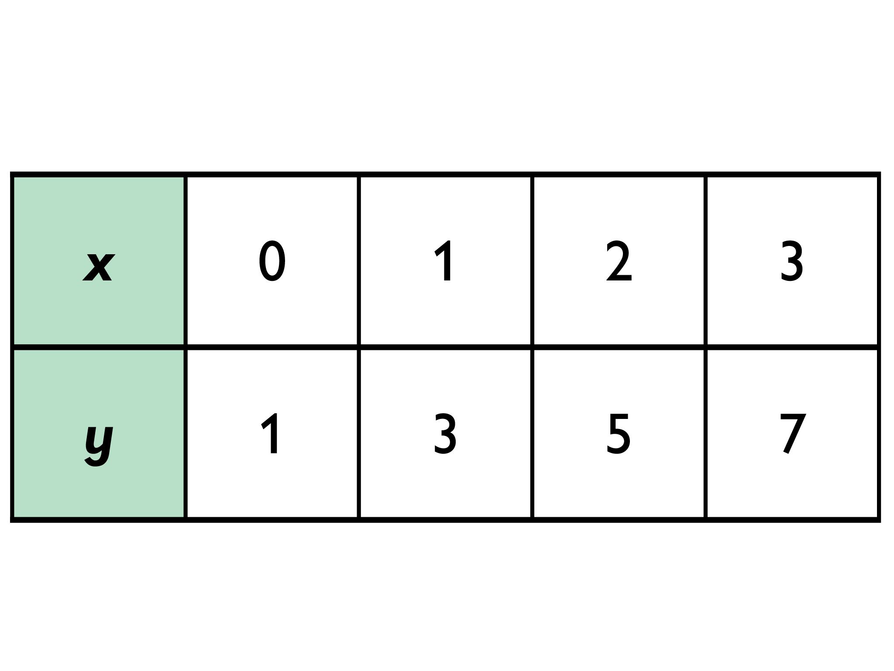
The table does not represent a proportional relationship because there is not a constant ratio between each pair of values; the graph does not pass through the point (0, 0).
Work Time
Prepare a Presentation
Prepare a presentation about the conclusions you reached about the three graphs.
Challenge Problem
- Make a graph using the values in the table.
- Does the graph/table represent a proportional relationship? Explain.
Make Connections
Mathematics
Use this part of the lesson to showcase a range of choices students made about the axes by having students who made different choices present their work.
Compare the three different graphs. Highlight the fact that the graphs in the first two problems are straight lines that pass through the point (0, 0), no matter which axis is chosen for each quantity in each problem. For each graph shared by a student, ask:
- Is the graph a straight line?
- Does it pass through the point (0, 0)?
- What do the different graphs of the relationship in this problem show? (Point to graphs where the x- and y-axes represent different quantities.) How are they different and how are they alike?
SWD: If you know that some students may need additional time or prompting to participate in this discussion, provide them several of the questions ahead of time (printed out or digitally).
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ comparisons of the three graphs.
Hint:
As your classmates present, ask questions such as:
- How did you decide what the x - andy -axes should represent?
- Can you explain the relationship between the x - and
y -axes? - Does your graph pass through the point (0, 0)?
- Would it make sense to connect the points on your graph? Think about the situation that the graph represents.
- Where in your graph do you see the numbers in the table?
Graphs of Proportional Relationships
Lesson Guide
- Have pairs quietly read and then discuss the information and the graphs shown.
- As student pairs work together, make a note to clarify any misunderstandings in the class discussion.
- After a few minutes, discuss the summary as a class. Discuss the following points:
- The graph of a proportional relationship is a straight line.
- Graphs help you visualize a relationship between two quantities better than tables or formulas.
- When you graph a relationship, you often have to make important decisions about the coordinate axes—for example, which quantity is represented by each, the scale of each, and which quadrant(s) are relevant—in order to show the relationship in a way that helps you see and understand it.
Formative Assessment
Summary of the Math: Graphs of Proportional Relationships
Read and Discuss
- The graph of a proportional relationship between two quantities is a straight line that starts at the origin, (0, 0).
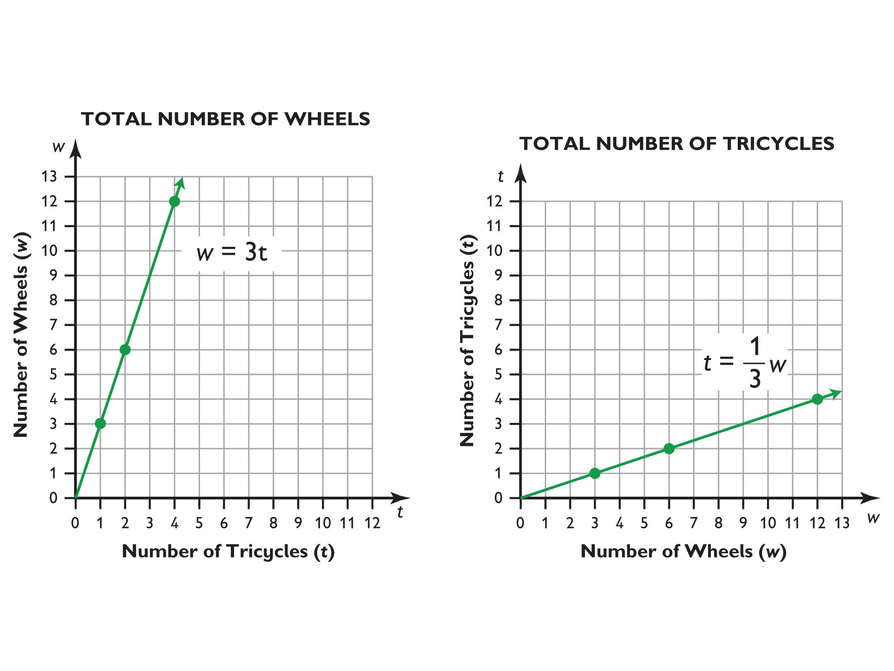
These graphs show the proportional relationship between tricycles and wheels.
- In the graph of w = 3t, the x-axis represents the number of tricycles (t). The y-axis represents the number of wheels (w).
- In the graph of , the x-axis represents the number of wheels (w). The y-axis represents the number of tricycles (t).
- In the first graph, there is a point at (1, 3), at (2, 6), at (4, 12), and so on.
- In the second graph, there is a point at (3, 1), at (6, 2), at (12, 4), and so on.
Hint:
Can you:
- Explain how to use a table of values to make a graph?
- Explain what the graph of a proportional relationship looks like?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out if students can tell when a graph represents a proportional relationship.
ELL: Since summarizing one’s learning entails such a high level of understanding of the topic and command of the language, allow ELLs additional time to come up with the summary. Encourage them to work in pairs if necessary. Allow students to use a dictionary.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One way I can tell that a graph represents a proportional relationship is …