- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Sales Tax
Creating Equations, Tables & Graphs

Overview
Students create equations, tables, and graphs to show the proportional relationships in sales tax situations.
Key Concepts
- The quantities—price, tax, and total cost—can each be known or unknown in a given situation, but if you know two quantities, you can figure out the missing quantity using the structure of the relationship among them.
- If either the price or the total cost are unknown, you can write an equation of the form y = kx, with k as the known value (1 + tax), and solve for x or y.
- If the tax is the unknown value, you can write an equation of the form y = kx and solve for k, and then subtract 1 from this value to find the tax (as a decimal value).
Building a general model for the relationship among all three quantities helps you sort out what you know and what you need to find out.
Goals and Learning Objectives
- Make a table to organize known and unknown quantities in a sales tax problem.
- Write and solve an equation to find an unknown quantity in a sales tax problem.
- Make a graph to represent a table of values.
- Determine the unknown amount—either the price of an item, the amount of the sales tax, or the total cost—in a sales tax situation when given the other two amounts.
Model with Mathematics
Mathematical Practices in Action
Mathematical Practice 4: Model with mathematics.
Have students watch the video and listen to the dialogue between Karen and Maya. This video shows students engaged in Mathematical Practice 4: Model with mathematics.
After students watch the video, discuss how setting up a table helped Karen and Maya solve the problem. Ask students if the equation they set up will serve as a good model for the problem.
Point out that writing an equation is often a very helpful way to model the mathematics in a problem. Elicit that there are other ways to model mathematics as well. For example, visual representations such as a diagram of a situation are very helpful.
Opening
Model With Mathematics
Watch the video to see Karen and Maya use a table and set up an equation to model the mathematics in a problem.
- How did setting up a table help Karen and Maya solve the problem?
- Karen and Maya modeled the problem with an equation. Does their equation reflect the problem?
VIDEO: Mathematical Practice 4
Math Mission
Lesson Guide
Discuss the Math Mission. Students will create equations, tables, and graphs to show the proportional relationships in sales tax situations.
Opening
Create equations, tables, and graphs to show the proportional relationships in sales tax situations.
Chen’s Pair of Shoes
Lesson Guide
Have students work in pairs on all problems and the presentation.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Look for students who are seeing connections between different representations of the situation and using them to better understand the behavior of the quantities in relation to each other.
Mathematical Practice 7: Look for and make use of structure.
Identify students who are using the structure of the relationships among quantities to reason about solutions that make sense.
ELL: When students work in pairs, the teachers is able to monitor individual student progress by listening to and recording student conversations and peer problem solving. This type of collaborative work gives ELLs the opportunity to use mathematical language and to engage in conversation with their peers.
Interventions
[common error] Student doesn’t correctly interpret the given table.
- Refer to Karen’s table at the beginning of the lesson. Notice where the missing information is. What is the missing information in the shoes problem?
[common error] Student doesn’t build a correct equation.
- Use the letter p to represent the price of an item, the letter t to represent the tax percent, and the letter c to represent the total cost.
- What should the tax percent be multiplied by to find the missing value?
[common error] Student writes a correct equation, but doesn’t correctly solve it.
- Does your solution make sense in this situation?
- The unknown amount is the starting amount, which is the price before tax. Does your solution make sense as the price of the shoes?
Student doesn’t recognize starting amounts and final amounts as variable quantities when asked to make a table or a graph.
- The tax percent is fixed in this situation. What are the two quantities that vary in relation to each other?
- There are many items for sale in the store, many with different prices. Each item can be represented by a pair of corresponding values: its price (starting amount) and its total cost including tax (final amount). Use the table to show some examples of pairs of corresponding values for different items that you make up. Use a graph to show lots of examples of points defined by corresponding values for different items.
Possible Answers
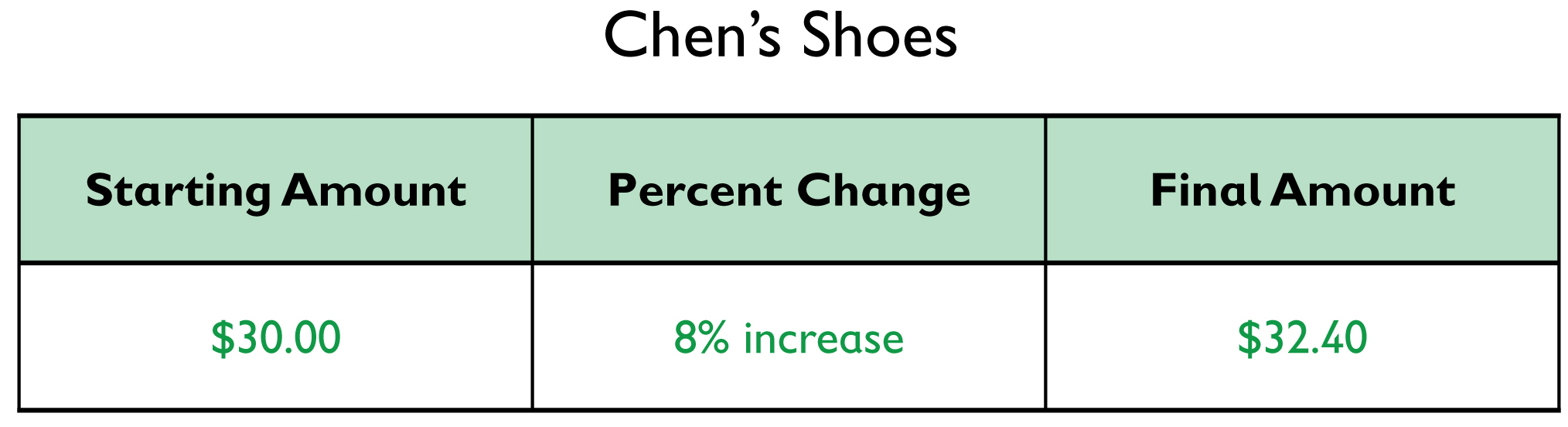
- 32.40 = (1.08)x
- x = 30
The price of the shoes was $30.
- Answers will vary. Possible answers:
Work Time
Chen’s Pair of Shoes
Chen bought a pair of shoes and paid a total of $32.40. The sales tax was 8%. What was the price of the shoes?
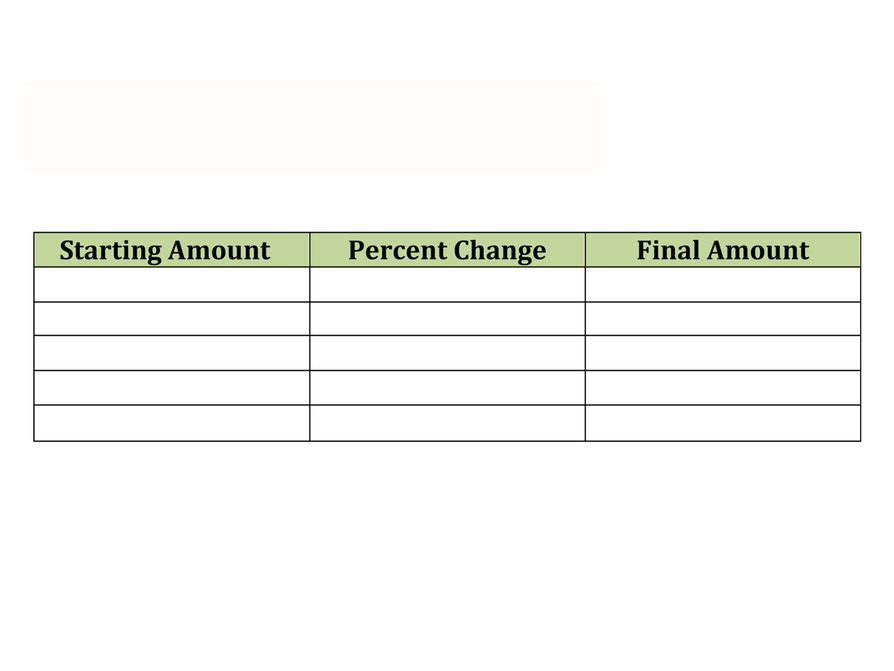
- Copy and complete the table. Show the information given in the problem, and what you need to find.
- Write an equation to find the price of the shoes.
- Solve the equation.
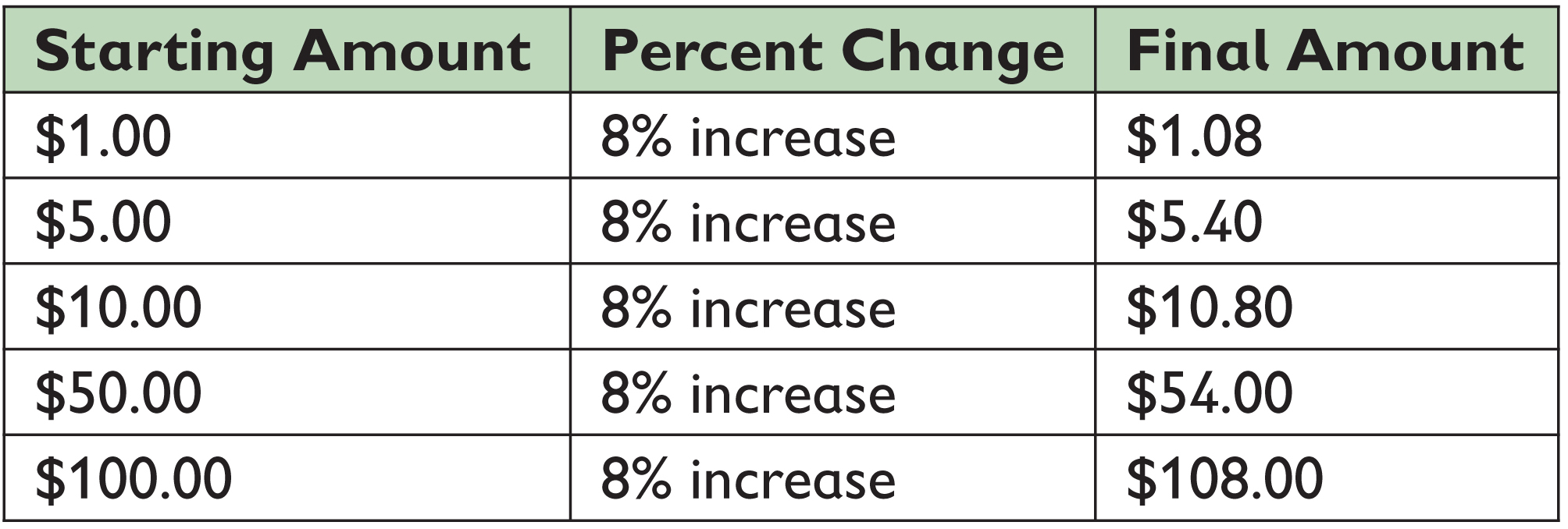
- Complete the given table to show the final amounts for different starting amounts.
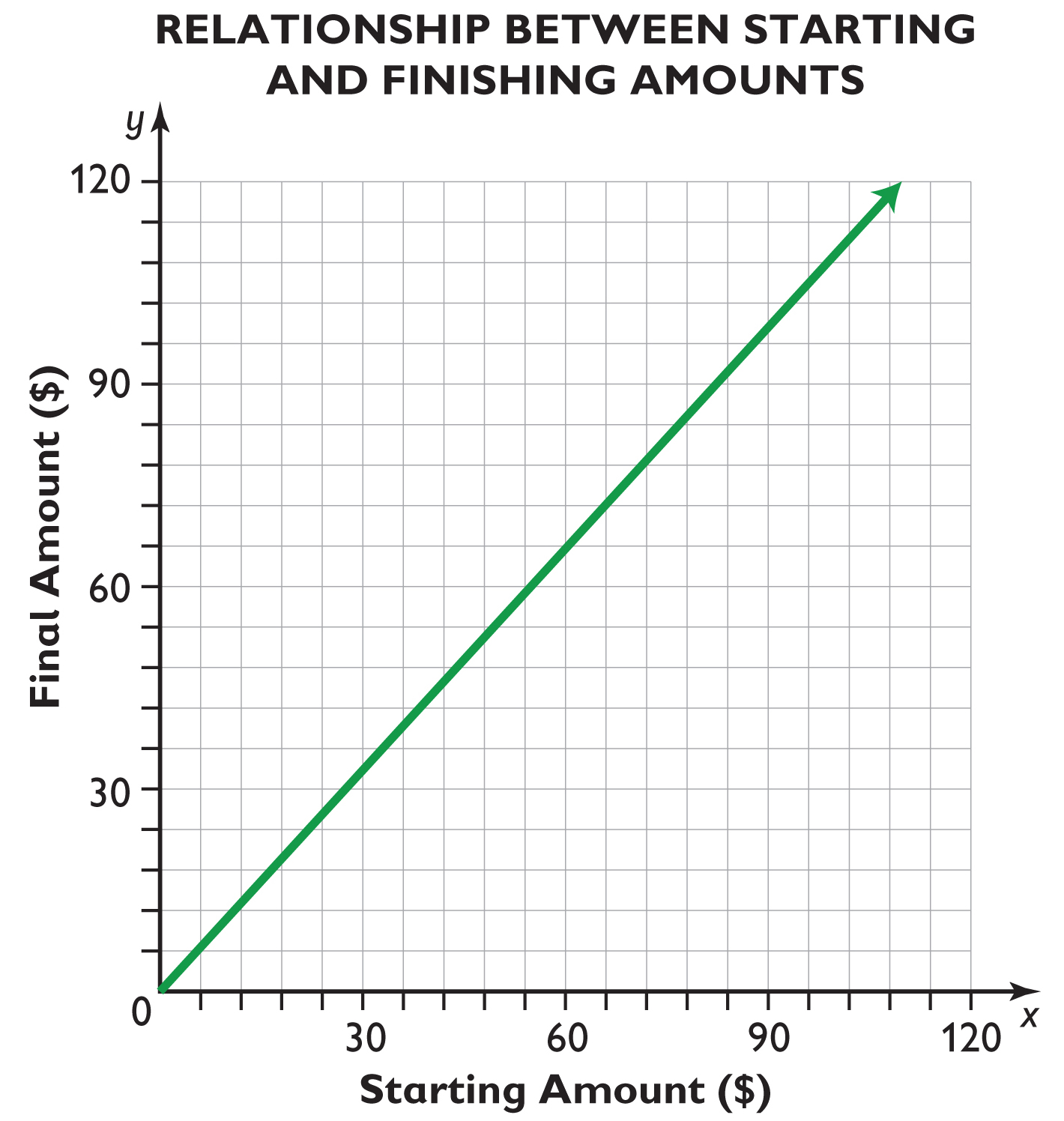
- Make a graph that shows the relationship between the starting amounts and the final amounts.
Hint:
- When you write the equation, how do you change the 8% to a decimal? What do you need to account for in your equation?
- Marcus wrote this equation: 1.08 • p = 32.40. Why did he multiply by 1.08? How could he write the equation differently?
- Once you have filled in the table with $32.40 including the 8% tax, how do you extend the table? What stays constant? What varies?
Sophie’s Book
Lesson Guide
Have students work on all problems and the presentation.
Answers
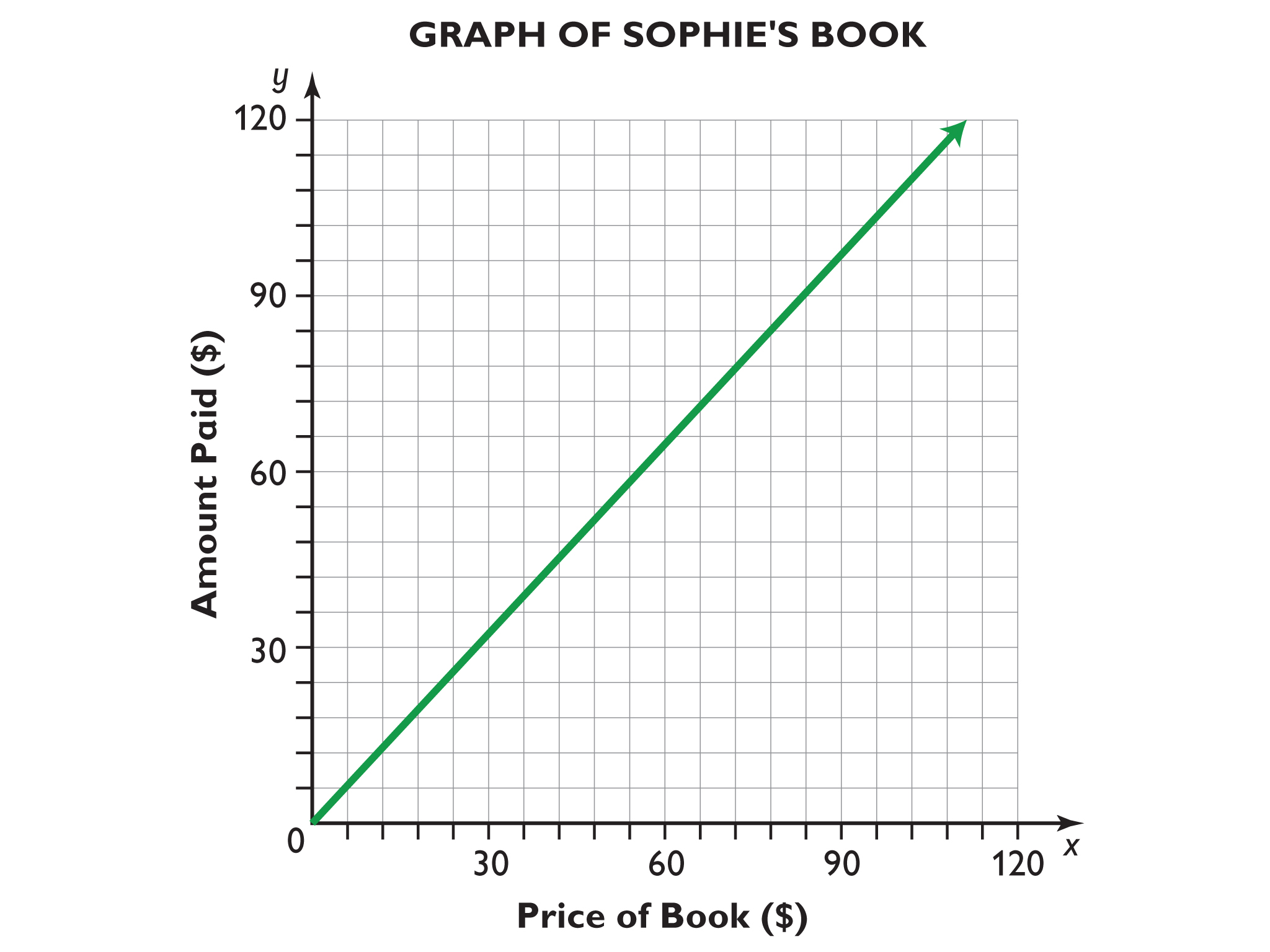
- Graph for Sophie's book
Work Time
Sophie’s Book
Recall the problem from the video:
Sophie bought a book at the bookstore. The price of the book was $18, and the total amount she paid was $19.08. What percent was the sales tax?
- Make a table of the relationships and fill in the first few rows.
- Make a graph that shows the relationship between the price of a book and the total amount paid.
HANDOUT: Sales Tax
Hint:
- Try filling in a table of different starting and final amounts that reflect a 6% tax. What stays constant? What varies?
- Once you have filled in several rows of the table, use the values to create your graph.
Prepare a Presentation
Preparing for Ways of Thinking
Look and listen for students who:
- Understand the role of the tax percent in relating the starting and final amounts.
- Understand that there are three quantities, each of which can be known or unknown.
- Use the structure of the relationship between quantities to find missing information.
- Easily graph the relationships in the problem situations, particularly setting up the axes.
Challenge Problem
Answers
- Answers will vary. Students should notice that the steepness of each graph is very similar; they may also notice which graph is steepest and which is least steep. At this point, they may not be able to say much about the value of the slope being very close to 1 in each case.
- The constants of proportionality are The Price and Total Cost of Items graph: 1.05; Buying a Book graph: 1.06; and Buying Shoes graph: 1.08.
Work Time
Prepare a Presentation
Prepare a presentation comparing what is similar and what is different between the book problem and the shoe problem.
Challenge Problem
- Look back at the graph you made in the previous lesson representing the relationship between the price and total cost of items at a 5% tax. Compare it to the two graphs you made in this lesson. If the scales on the axes of any of the graphs are different, re-create the three graphs on the same coordinate plane.
- How does the steepness of each graph compare with the steepness of the other graphs? Identify the constant of proportionality in each relationship.
Make Connections
Lesson Guide
Highlight the connections made by students between the two situations in this lesson and the situation in the previous lesson. Use student work on the Challenge Problem to stimulate a discussion that makes these connections explicit if student presentations on the other problems aren’t enough to do so. All three relationships have the same quantities and same structure, but in the buying a book situation, the unknown amount was the tax. Karen used the structure of the relationship to find the tax percent.
ELL: As ELLs explain their reasons verbally and in writing, their answers may have language errors. Remember, language mistakes are natural.
- Focus on the content being communicated.
- Allow processing time.
- Do not emphasize grammar.
- Model standard English.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Be sure to publicly recognize student contributions that illustrate general practices that are good for modeling quantitative relationships.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ graphs and comparisons.
Hint:
As your classmates present, ask questions such as:
- How did the table help you make a graph of the situation?
- How does the line change as the sales tax changes in the different graphs? Can you explain the change?
- Why did you multiply by 1 plus the sale tax?
- Does your solution make sense in this situation?
- Could you have predicted what the graph would look like before you made it? How?
- Why do you think you found those similarities between the graphs?
- Why do you think you found those differences between the graphs?
- Are there any conclusions you can make based on comparing the graphs?
Percent Change
Lesson Guide
Have pairs quietly read and then discuss the two ways to calculate a percent increase. As student pairs work together, make a note to clarify any misunderstandings in the class discussion.
After a few minutes, discuss the summary as a class. Be sure to include the following points:
- In a sales tax situation, the unknown can be the sales tax, the amount of the tax, the starting price, or the total cost.
- A table can help you organize what is given in the problem and what you need to find.
- You can make a table and/or a graph to show the relationships in a sales tax situation.
SWD: Students with disabilities may need additional support seeing the relationships among problems and strategies. Throughout this unit, keep anchor charts available and visible to assist them in making connections and working toward mastery. Provide explicit think-alouds comparing strategies and making connections. In addition, ask probing questions to get students to articulate how a peer solved the problem or how one strategy or visual representation is connected or related to another.
Formative Assessment
Summary of the Math: Percent Change
Read and Discuss
- A percent can describe a change in a value—for example, a percent increase.
- If a value increases by x%, you can calculate the new value in two ways:
- Calculate x% of the original amount and add the result to the original amount.
- Calculate (100% + x%) of the original amount.
- For example, if the percent increase is 5% and the original amount is m, then:
0.05 + m = the total amount, or 1.05m = the total amount - These two equations are equivalent because:
0.05m + m = 1.05m
0.05m + 1m = 1.05m(0.05 + 1)m = 1.05m
Hint:
Can you:
- For a problem about a sales tax situation, create a table that can help you organize what is given and what you need to find?
- Use a table to make a graph?
- Determine one of the amounts in a sales tax situation—the price of an item, the amount of the sales tax, or the total cost—if you know the other two amounts?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out what helped students the most in solving the sales tax problems.
SWD: Some students with disabilities may struggle to explain their mathematical reasoning in words. Provide sentence starters or paragraph frames to support students with this task.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
What helped me most in solving today’s sales tax problems was …