- Author:
- Pearson
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Guess the Colors
Number Cube
Spinner
Experimental Probability

Overview
Lesson Overview
Students will extend their understanding of probability by continuing to conduct experiments, this time with four-colored spinners. They will compare experimental results to expected results by first conducting an experiment, then calculating the probability of an event.
Key Concepts
- This lesson takes an informal look at the Law of Large Numbers, comparing experimental results to expected results.
Goals and Learning Objectives
- Learn about experimental probability.
- Compare theoretical probability to experimental probability and show that experimental probability approaches theoretical probability with more trials.
- Use proportions to predict results for a number of trials.
Number Cube Results
Lesson Guide
Use the Number Cube interactive to demonstrate and show the total number of rolls for each number from the number cube trial. Show the class data you collected in the previous lesson from the informal class poll. Students will briefly discuss things they noticed.
Ask students if they knew the data for all the rolls of the class, how could the outcomes change? Could they predict the outcome for 900 rolls?
Mathematics
Students should see that the numbers are pretty close to each other because the probability of each number is the same. They may also notice that the numbers are closer to each other than results for their 30 rolls.
Explain that the actual results, the results of the experiment, give us the experimental probability, or the ratio of favorable outcomes to the total number of trials. The theoretical probability is defined as the ratio of favorable outcomes to the total number of possible outcomes, often simply called probability. Therefore, in this example, it is , so now we can compare and see that the experimental probability is not far from the theoretical probability.
Ask students if the results make sense:
- How do these results compare with your predictions?
- How did these results compare with the results for your 30 rolls?
- Were the results closer to what was expected for your 30 rolls or the entire class' results?
- What do you think would happen if there were 9,000 rolls?
SWD: Though informal, discuss as an introduction/preview for students with disabilities. Emphasize key information/critical concepts that will be introduced. This will support students as they work to determine salient information throughout the lesson.
Opening
Number Cube Results
The Number Cube interactive can show the results for rolling the number cube 30 times for each number on the number cube. Discuss the following questions.
- What do you notice about the numbers?
- How do these numbers compare with class data?
INTERACTIVE: Number Cube
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore experimental probability using spinners.
Opening
Explore experimental probability using spinners.
Work With Spinners
Lesson Guide
Students will work individually to conduct the experiment.
Mathematics
Students should have a rough idea of the proportions of each section compared to the whole circle. They don't know what the actual proportions are, so they will establish the probability by accumulating trials. Students should also notice that the probabilities must add to 1 (or 100%) and take this into account as they predict and calculate.
SWD: Students who struggle with mathematical understanding may need explicit explanation of the connections between this new concept and previously learned concepts. Ask scaffolding questions to promote student “discovery” of the connections between theoretical and experimental probability.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students must make sense of problems in order to both solve and create them.
Interventions
Student has trouble getting started.
- How many outcomes were there for each color?
- How many total trials were there?
- How can you compare these numbers as a ratio?
Student's answers for the outcomes appear random, or not based on ratios.
- How did you decide on these numbers?
- What fraction of the circle (roughly) is yellow?
- How many yellow sections would fit in the whole circle?
Possible Answers
- Answers will vary. Possible answer:
- Blue: 20 times
- Red: 10 times
- Yellow: 15 times
- Green: 55 times
NOTE: In this possible answer, the spinner lands on green more than 50 times, the spinner lands on green most often, the spinner lands on red the least often, and the total number of spins adds to 100. All answers should have these characteristics.
- Answers will vary and will depend on the results of the students' experiments and their answers to the previous part of the problem.
- Answers will vary and will depend on the results of the students' experiments.
Work Time
Work With Spinners
Look at the spinner provided in the interactive.
- Predict how many times the spinner would land on each color if it were spun 100 times.
blue, red, yellow, green - Spin the spinner 100 times. How do your actual results compare to your predictions?
- Use your results to calculate the experimental probability of each color.
INTERACTIVE: Spinner
Make Four Spinners
Lesson Guide
Students work with a partner to make the four spinners, predict results for each spinner, and use the results to find the experimental probability of each spinner.
Mathematics
Look at how students are predicting results. Are they guessing (or basing their guess on what they think will happen), or trying to use proportions? Also look at how students are finding the experimental probability for each spinner, including the spinner where red is certain.
Mathematical Practices
Mathematical Practice 5: Use appropriate tools strategically.
- The unit contains interactives and handouts that students will use to conduct experiments. In this lesson, students create spinners to test, create, and predict various theoretical probabilities.
- ELL: For this task, encourage students to explain their ideas to one another. Math language must be used. Encourage the use of English without discouraging students from using their first language(s).
Answers
There are many possible answers for this problem. Calculations for theoretical and experimental probabilities depend on the spinner constructed and the experimental results. A few possible spinners:
- The spinner should have equals areas of red and blue and a very small area for yellow. The remainder is left for green.
- Red, blue, and green are equal in size, with the remainder left for yellow.
- The area for red must be twice that for blue, and four times that for green. The remainder is left for yellow.
- The spinner is predicted to land on red 100 out of 100 times. The experiment should result in 100 spins landing on red.
Work Time
Make Four Spinners
Using the Creating Spinners interactive, work with a partner to make spinners that will give the following results. For each spinner, predict the results for 100 spins. Then spin 100 times and use your results to find the experimental probability of each color.
- The spinner is equally likely to land on red and blue, and unlikely to land on yellow.
- The spinner is equally likely to land on red, blue, and green.
- The spinner is twice as likely to land on red as it is to land on blue, and is twice as likely to land on blue as it is to land on green.
- The spinner is certain to land on red.
INTERACTIVE: Creating Spinners
Guess the Colors
Lesson Guide
Students will work with a partner.
Interventions
Student has trouble predicting the hidden spinner.
- How do the results for each color compare to each other?
- What does that tell you about the probability of each color?
Answers
- Answers will vary. Answers will depend on the spinner constructed and the experimental results.
Work Time
Guess the Colors
Use the Guess the Colors interactive.
- Make a spinner that your partner cannot see.
- Spin the spinner 100 times. Tell your partner the results. Hide the colors of the spinner. Your partner should try to describe what the spinner looks like based on the results and choose each color.
- Your partner can spin more times if needed to determine what the size of the colored areas on the spinner look like.
Prepare a Presentation
There are many possible spinners for the problem with the criteria as listed, so look for different approaches to share in Ways of Thinking. For example, some students will realize that they will have a better chance of having their prediction match the actual results in number one if the red and blue sections are both small.
Look at how students are predicting results. Are they guessing (or basing their guess on what they think will happen), or trying to use proportions? Also look at how students are finding the experimental probability for each spinner, including the spinner where red is certain.
Presentations will vary. Presentations should:
- Note the differences between theoretical and experimental probability.
- Use examples to support findings.
Look for students who did the Challenge Problem to present during Ways of Thinking.
Challenge Problem
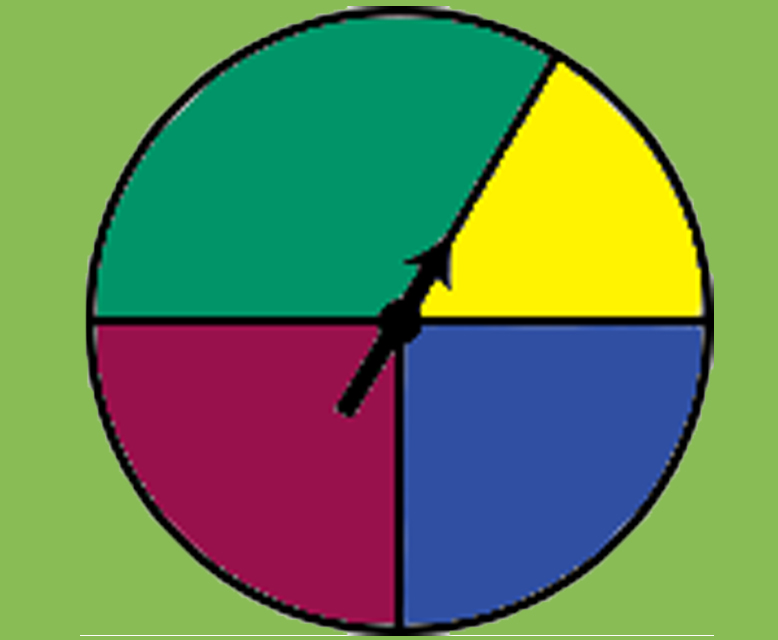
Answers
- The experimental probabilities for this spinner: P(red) = 25.7%
P(yellow) = 17.0%
P(blue) = 24.4%
P(green) = 32.9%
P(red) and P(blue) are very close to 25%, which is . P(yellow) is close to , which is %. P(green) is close to , which is %.
Work Time
Summarize what you learned from your work with spinners. Provide examples to illustrate your conclusions.
Challenge Problem
In 1,000 spins, a spinner lands on red 257 times, yellow 170 times, blue 244 times, and green 329 times.
- If the probability of each color can be shown with a unit fraction, what does the spinner probably look like?
Make Connections
Lesson Guide
As students present, encourage the rest of the class to ask questions, using the Hints as a guide.
Mathematics
While students are presenting about the first spinner, use these questions to help guide the conversation:
- What is the theoretical probability for each color?
- How did you calculate these probabilities?
- What are the experimental probabilities of your experiment?
- How do the experimental probabilities compare with the theoretical probabilities?
While students are presenting the spinners created with given parameters, ask these questions:
- How did you decide how to make each spinner?
- What factors did you consider and what did this tell you about the probability of each color?
- Were the results for 100 spins what you expected?
- Why do you think this happened?
- Which spinner was the easiest to test?
- Are 100 trials enough to establish the probabilities? Why?
While students are presenting the spinners that they created, ask these questions:
- Were 100 spins enough to predict what your partner's spinner looked like?
- How did you decide what the spinner looked like?
- ELL: As with other discussions, encourage ELLs to use the academic vocabulary they have learned. Introduce new vocabulary as needed. As they participate in the discussion, be sure to monitor for knowledge of the topic.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- When comparing predicted and actual results, students must make sense of the information and construct arguments about their observations.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ observations and explanations regarding experimental probability based on their work with spinners.
Spinners and Probability
A Possible Summary
You can calculate experimental probability by running an experiment and looking at the actual results. For the spinner, you can do this by dividing the number of times a color appears by the total number of spins. The more trials conducted, the closer experimental probability approaches theoretical probability.
- ELL: Ask ELL pairs to repeat the summary of math to each other in either their language of origin first or English. ELLs should choose the language that they feel most comfortable with.
Formative Assessment
Summary of the Math: Spinners and Probability
Write a summary about spinners and probability.
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out what students consider to be the difference between experimental and theoretical probability.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I think the difference between experimental probability and theoretical probability is…