Math I: Corralling the Sheep - Exploring Linear Equations

Overview
Students are given 4-5 coordinate points, that will represent the sheep. First, they are tasked with creating a fence around the sheep. The students will use the endpoints of each piece of fence to compute the slope, y-intercept, domain and equation of the line. They will then code the rover to draw their lines. Finally, the students can calculate the area/perimeter of their fence and calculate the cost to build the fence. The students will then be challenged to minimize the area, perimeter and cost of building their corral, recalculate the equations of their lines, stating their new slope, y-intercept, and domain.
Instructor Directions
Project Description | |
| Name of Project | Corralling the Sheep - Exploring Linear Equations |
| Subject Area | Math 1 |
| Targeted Standards | NC.M1.A-CED.1 - Create equations in one variable that represent linear relationships and use them to solve problems.NC.M1.F-LE.5 - Interpret the parameters a and b in a linear function f(x)=ax+bNC.M1.G-GPE.4 - Use coordinates to solve geometric problems involving polygons algebraically
|
| Driving Question / Problem / Activator | Can you create a fence around given coordinate points (sheep) that will minimize the area of the polygon? |
| Project Summary | Students are given 4-5 coordinate points, that will represent the sheep. First, they are tasked with creating a fence around the sheep. The students will use the endpoints of each piece of fence to compute the slope, y-intercept, domain and equation of the line. They will then code the rover to draw their lines. Finally, the students can calculate the area/perimeter of their fence and calculate the cost to build the fence. The students will then be challenged to minimize the area, perimeter and cost of building their corral, recalculate the equations of their lines, stating their new slope, y-intercept, and domain. |
| Estimated Time | 1-2 class periods (1.5 hours each) |
| Materials / Resources (including link to slideshow if available) | *Assignment worksheet, including rover code*large grid paper*Skinny dry erase marker*Ti Innovator hub and rover*Ti 84 Plus CE calculators*Cotton balls for sheep |
| Tags | Linear EquationsSlopeMinimizing distanceAreaMinimizing cost |
Project Outline | |
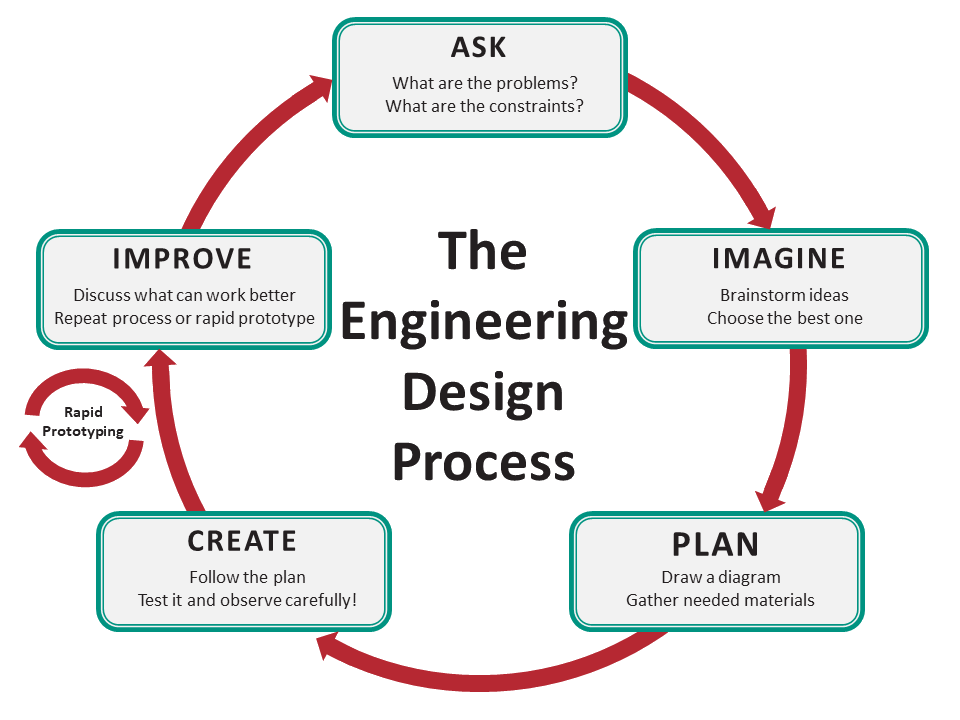
| Ask | Students will create and write linear equations, with restricted domains, to create a polygon that encompasses given coordinate points. |
| Imagine | Students will draw their corral on paper and identify their potential endpoints to use. |
| Plan | Students will then begin calculating the features of their equations, including slope, y-intercept, and domain. |
| Create | Students will write their equations, program them into the rover, and correctly input the key features into the program. The rover will draw the lines that have been entered. |
| Improve | Students will be challenged to minimize the amount of fencing they use, area of their corral, and cost of their materials. |
| Closure / Student Reflections | Students will reflect on how the key features are related to the endpoints of the lines, and how the area/perimeter are affected by changing the features of each line. |
| Possible Modifications / Extensions | Teachers could add restrictions to make the task more challenging, including requiring the students to include a pair of parallel lines, giving the students a budget to adhere to or giving the students a specific shape for their corral. |
Evaluation (Pre/Post)
Insert Links to Google Forms
Pretest Link:
Post-test Link:
Credits or Modified From
Texas Instruments: Leveraging TI Innovator Rover in the Math Classroom
Additional Resources / Help for teaching this lesson
Pretest Link:
Posttest Link:
Sample Pictures / Video
Teacher Comments of what worked / did not work well