- Author:
- William Allred, Carrie Robledo
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Level:
- High School
- Tags:
- License:
- Creative Commons Attribution Non-Commercial Share Alike
- Language:
- English
Education Standards
Teacher Instructions - Laws of Sines and Cosines.docx
Teacher Instructions - Vectors.docx
9-12 Math: Sum and Differences of Vectors

Overview
Students will resolve vectors into x and y-components, combine these values to determine the components of the resultant, and determine the magnitude and direction of the resultant.
Instructor Directions
Project Description | |
| Name of Project | Sum and Differences of Vectors |
| Subject Area | Math |
| Targeted Standards | 2003 NC Standard Course of StudyPreCalculus: Objective 1.03 Operate with vectors in two dimensions to model and solve problems.Revised NC 4th Math CurriculaPreCalculus: NC.M4.N2.2 |
| Driving Question / Problem / Activator | How do resolve vectors to component form and determine resultants? How do you determine the magnitude and direction of resultant vectors? How can robots be used to reinforce students’ understanding of these relationships? |
| Project Summary | Students will resolve vectors into x and y-components, combine these values to determine the components of the resultant, and determine the magnitude and direction of the resultant. |
| Estimated Time | This lesson is designed to be presented during a standard 90 minute class. |
| Materials / Resources/Lesson Plans (including link to slideshow if available) | Sphero Robots, Masking Tape, Tape measure, Sharpie Markers; Students will need pencils, paper, and calculators.https://drive.google.com/open?id=1kLbfNdFLZQwAjK4xz1iMp9Csyep88N1Hhttps://drive.google.com/open?id=1GSyK6DQacTas-sJ9XDg5OIywMZCujT0S |
| Tags | |
Project Outline | |
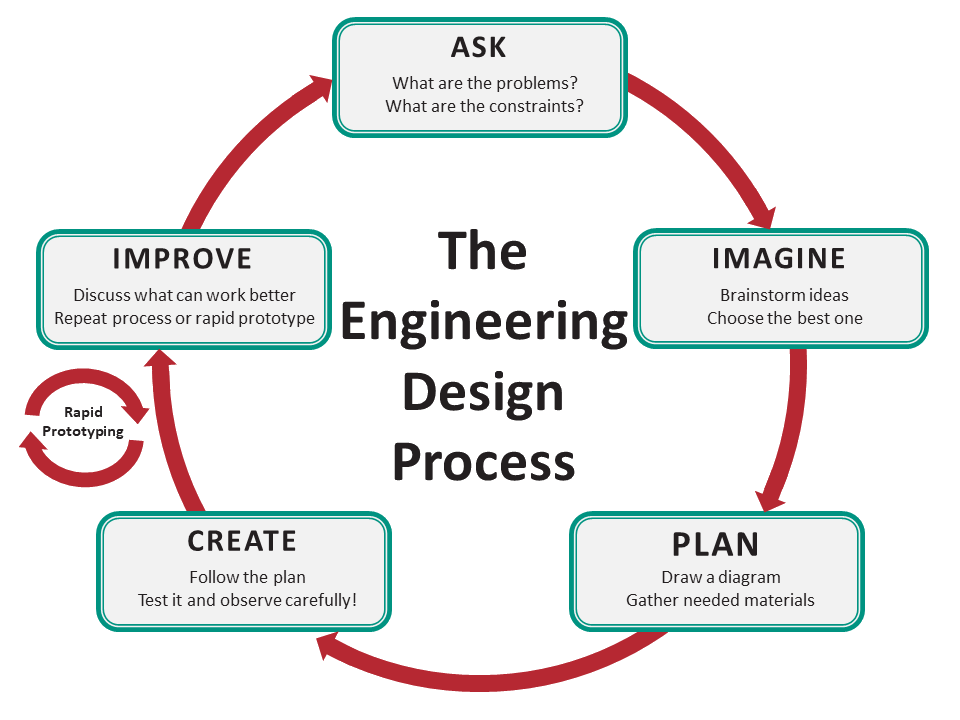
| Ask | How do you resolve vectors to component form and determine resultants? How do you determine the magnitude and direction of resultant vectors? Can robots be used to reinforce students’ understanding of these relationships? |
| Imagine | How could this activity be be accomplished using different types of robots? Other types of robots are more precise in their movements, but Spheros are easy to program and relatively inexpensive. |
| Plan | Students will calculate travel times and directions necessary to traverse vectors. |
| Create | Students will program their robots to traverse the individual vectors, as well as the resultant vectors. |
| Improve | Determine improvements to the layout of the work area, sequence of instructions, wording of narrative and instructions |
| Closure / Student Reflections | 1) How closely did the robot’s stopping point at the endpoint of each resultant vector agree with the sum/difference of the given vectors?3) After observing robots’ response to programmed directions, what program revisions could be made to improve accuracy?2) What sources of error might affect the accuracy of a robot’s travel? |
| Possible Modifications / Extensions | Evaluate the effect of travel speed on the accuracy of travel. Evaluate the effect of different surfaces on the accuracy of travel. |
Evaluation (Pre/Post)
At the start of the activity:
After the activity:
1) How far apart were the endpoints of the resultant vectors from the final endpoint of the component vectors?
Activity A Activity B Activity C
2) Evaluate the following sources of error on the accuracy of a robot’s travels.
a. How does a robot’s initial alignment affect the accuracy of each activity?
b. Speed; Suppose a robot’s actual speed is faster or slower than accounted for in your calculations. Determine the error in distance traveled over 15 seconds for the following speed errors. (Show two sample calculations.)
| Speed Error | Travel Error | Speed Error | Travel Error |
| + 0.1 in/sec | – 0.1 in/sec | ||
| + 0.15 in/sec | – 0.15 in/sec | ||
| +0.5 in/sec | – 0.5 in/sec | ||
| + 1 in/sec | – 1 in/sec |
c. Direction/Angle; Suppose a robot’s direction differs from the “correct” direction. Given a triangle with two sides that are each 15 ft, determine the error in the “third” side of the triangle that results from the following errors in the “included” angle. (Show two sample calculations.)
| Direction Error | “3rd Side” Error | Direction Error | “3rd Side” Error |
| + 0.5O | – 0.5O | ||
| + 1O | – 1O | ||
| + 3O | – 3O | ||
| + 5O | – 5O |
3) What other sources of error might affect the results of these activities?
4) Using the speed settings from the three triangles, determine the roll durations and headings/bearings necessary to verify the resultant sum of the following vectors.
Given:
Find the resultant: