Read the Fine Print
Interactive tool that allows user to transform functions and see effects on domain and range.
- Subject:
- Mathematics
- Material Type:
- Interactive
- Provider:
- GeoGebra
- Date Added:
- 05/31/2018
Updating search results...
38 Results
Conditional Remix & Share Permitted
CC BY-SA
Ana Donevska Todorova Humboldt Universitﾊt zu Berlin Mathematisch-Naturwissenschaftliche Fakultﾊt II Institut fﾟr Mathematik, Didaktik der Mathematik
- Subject:
- Algebra
- Mathematics
- Material Type:
- Simulation
- Provider:
- GeoGebra
- Provider Set:
- GeoGebraTube
- Date Added:
- 03/12/2012
Read the Fine Print
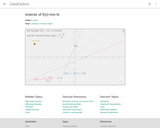
Interactive tool that allows one to see how the inverse of y=mx+b changes when the slope changes.
- Subject:
- Mathematics
- Material Type:
- Interactive
- Provider:
- GeoGebra
- Date Added:
- 05/31/2018
Read the Fine Print
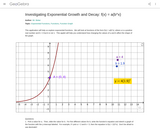
Interactive geogebra activity all about geometric growth and decay.
- Subject:
- Mathematics
- Material Type:
- Interactive
- Provider:
- GeoGebra
- Date Added:
- 05/30/2018
Read the Fine Print
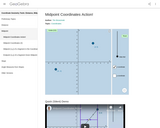
Geogebra activity that allows students to physically see the midpoint and endpoints of a segment.
- Subject:
- Mathematics
- Material Type:
- Interactive
- Provider:
- GeoGebra
- Date Added:
- 05/31/2018
Conditional Remix & Share Permitted
CC BY-SA
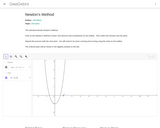
This models Newton's Method using a custom tool.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Simulation
- Provider:
- GeoGebra
- Provider Set:
- GeoGebraTube
- Date Added:
- 04/26/2012
Conditional Remix & Share Permitted
CC BY-SA
A visual demo of Newton's Method for pre-calculus students.
- Subject:
- Calculus
- Geometry
- Mathematics
- Material Type:
- Simulation
- Provider:
- GeoGebra
- Provider Set:
- GeoGebraTube
- Date Added:
- 04/26/2012
Conditional Remix & Share Permitted
CC BY-SA
This shows how Newton's method (also known as Newton-Raphson) is used to find a root of a function. You can show/hide various parts of the construction, and edit the particular function being considered.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Simulation
- Provider:
- GeoGebra
- Provider Set:
- GeoGebraTube
- Date Added:
- 03/12/2012
Read the Fine Print
Interactive application of a piecewise function.
- Subject:
- Mathematics
- Material Type:
- Interactive
- Provider:
- GeoGebra
- Date Added:
- 05/31/2018
Read the Fine Print
This interactive resource allows a teacher or student to manipulate the vertices of the triangle to investigate the location of the centers of a triangle.
- Subject:
- Mathematics
- Material Type:
- Interactive
- Provider:
- GeoGebra
- Date Added:
- 05/31/2018
Conditional Remix & Share Permitted
CC BY-SA
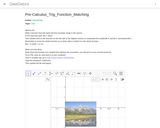
Students will create their own sine function to match a picture of mountains. This will teach them what the coefficents of trig functions do.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Simulation
- Provider:
- GeoGebra
- Provider Set:
- GeoGebraTube
- Date Added:
- 03/12/2012
Read the Fine Print
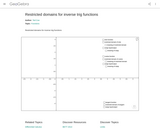
Interactive tool to see how the domains of trig functions need to be restricted for an inverse to exist.
- Subject:
- Mathematics
- Material Type:
- Interactive
- Provider:
- GeoGebra
- Date Added:
- 05/31/2018
Read the Fine Print
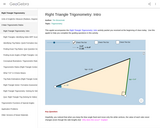
Geogebra interactive resource using trig properties.
- Subject:
- Mathematics
- Material Type:
- Interactive
- Provider:
- GeoGebra
- Date Added:
- 05/31/2018
Read the Fine Print
Goegebra activity demonstrating rigid transformations.
- Subject:
- Mathematics
- Material Type:
- Interactive
- Provider:
- GeoGebra
- Date Added:
- 05/31/2018
Conditional Remix & Share Permitted
CC BY-SA
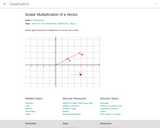
Simply shows multiplication of a vector by a scalar. Adjust he slider to adjust the multiple. Drag the point at the end of vector v to change the original vector.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Simulation
- Provider:
- GeoGebra
- Provider Set:
- GeoGebraTube
- Date Added:
- 03/12/2012
Conditional Remix & Share Permitted
CC BY-SA
This is a solver for problems involving the time value of money (TVM). It emulates the TVM solver on the TI-83+ and TI-84 graphing calculators. Updated 6 November 2011 to work correctly when I% = 0.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Simulation
- Provider:
- GeoGebra
- Provider Set:
- GeoGebraTube
- Date Added:
- 04/26/2012
Conditional Remix & Share Permitted
CC BY-SA
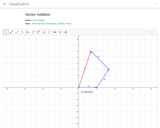
Addition of three Vectors, and displays resultant Vectors. Can drag the endPoints of the three different Vectors, but the resultant always starts at the origin.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Simulation
- Provider:
- GeoGebra
- Provider Set:
- GeoGebraTube
- Date Added:
- 03/11/2012
Conditional Remix & Share Permitted
CC BY-SA
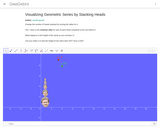
My pre-Calculus students were having trouble visualizing what it meant for a geometric series to converge. They understood the formula aspect and how to calculate the value of a convergent sum, and saw what it meant for numbers adding successively, but I
- Subject:
- Geometry
- Mathematics
- Material Type:
- Simulation
- Provider:
- GeoGebra
- Provider Set:
- GeoGebraTube
- Date Added:
- 06/25/2012