Great Visuals to clarify the abstract concepts of states of matter and how temperature affects states of matter.
This interactive activity demonstrates and provides explanation for how acid rain affects aquatic ecosystems and how certain species react to decreased water quality as pH becomes lower. The activity also explains the pH scale as a measure of acidity.
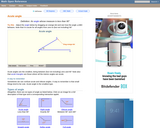
An interactive applet and associated web page that demonstrate acute angles (those less than 90 deg). The applet presents an angle (initially acute) that the user can adjust by dragging the end points of the line segments forming the angle. As it changes it shows the angle measure and a message that indicate which type of angle it is. There a software 'detents' that make it easy capture exact angles such as 90 degrees and 180 degrees The message and angle measures can be turned off to facilitate classroom discussion. The text on the page has links to other pages defining each angle type in depth. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
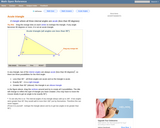
An interactive applet and associated web page that demonstrate the three types of triangle: acute, obtuse and right. The applet shows a triangle that is initially acute (all angles less then 90 degrees) which the user can reshape by dragging any vertex. There is a message changes in real time while the triangle is being dragged that tells if the triangle is an acute, right or obtuse triangle and gives the reason why. By experimenting with the triangle student can develop an intuitive sense of the difference between these three classes of triangle. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
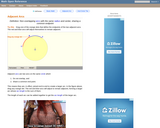
An interactive applet and associated web page that demonstrate the the concept of adjacent arcs. The user can 3 drag points around a circle that define the endpoints of two adjacent arcs. Web page has the properties of adjacent arcs. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
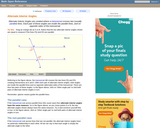
An interactive applet and associated web page that demonstrate the alternate interior angles that are formed where a transversal crosses two lines. The applets shows the two possible pairs of angles alternating when in animation mode. By dragging the three lines, it can be seen that the angles are congruent only when the lines are parallel. When not in animated mode, there is a button that alternates the two pairs of angles. The text on the page discusses the properties of the angle pairs both in the parallel and non-parallel cases. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
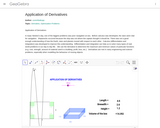
We use the derivative to determine the maximum and minimum values of particular functions (e.g. cost, strength, amount of material used in a building, profit, loss, etc.).Differentiation is also used in analysis of finance and economics.
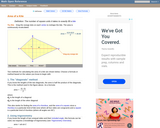
An interactive applet and associated web page that demonstrate the area of a circle. A circle is shown with a point on the circumference that can be dragged to resize the circle. As the circle is resized, the radius and the area computation is shown changing in real time. The radius and formula can be hidden for class discussion. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
An interactive applet and associated web page that deals with the area of a kite, (a quadrilateral with two distinct pairs of equal adjacent sides). The applet shows a kite and the user can reshape it by dragging any vertex. The other vertices move automatically to ensure it always remains a kite. As the vertices are dragged, the area is continuously recalculated and displayed. The kite is filled with a grid of unit squares so that the students can estimate the area. The on-screen calculation can be hidden until the estimates are done. The web page lists two different ways to compute the area of a kite. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
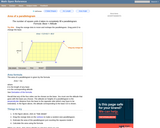
A web page and interactive applet showing the ways to calculate the area of a parallelogram. The user can drag the vertices of the parallelogram and the other points change automatically to ensure it remains a parallelogram. A grid inside the shape allows students to estimate the area visually, then check against the actual computed area, which is continuously recomputed and displayed. The text on the page gives three different ways to calculate the area with a formula for each. The applet uses one of the methods to compute the area in real time, so it changes as the rhombus is reshaped with the mouse. A companion page is http://www.mathopenref.com/parallelogram.html showing the definition and properties of a parallelogram Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
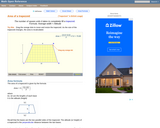
A web page and interactive applet showing the ways to calculate the area of a trapezoid. The user can drag the vertices of the trapezoid and the other points change automatically to ensure it remains a trapezoid. A grid inside the shape allows students to estimate the area visually, then check against the actual computed area. The text on the page gives three different ways to calculate the area with a formula for each. The applet uses one of the methods to compute the area in real time, so it changes as the trapezoid is reshaped with the mouse. A companion page is http://www.mathopenref.com/trapezoid.html showing the definition and properties of a trapezoid. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
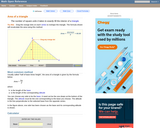
An interactive applet and associated web page that explain the area of a triangle. The applet shows a triangle that can be reshaped by dragging any vertex. As it changes, the area is continually recalculated using the 'half base times height' method. The triangle has a fixed square grid in its interior that can be used to visually estimate the area for later correlation with the calculated value. The calculation can be hidden while estimation is in progress. The text page has links to a similar page that uses Heron's Formula to compute the area. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
The simulation shows a ballistics cart. If the cart is at rest on a horizontal surface, it will shoot a ball straight up in the air, and catch the ball again. What if, as in this simulation, the cart is traveling at a constant velocity horizontally, instead? Will the ball land ahead of the cart, in the cart, or behind the cart? Note that the cart fires the ball straight up, with respect to the cart, when the middle of the cart passes the small vertical trigger on the track.
Use the buttons to select the different modes (whether there is a tunnel or not, and whether to show the velocity vectors).
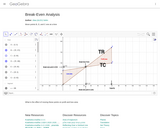
Break-Even analysis and the effect of changing Fixed costs, Variable Costs, and Selling price on Profit/Loss
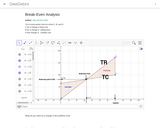
Try to move points (one at a time) C, B, and D C for a change in fixed cost B for a change in selling price D fora change in variable cost
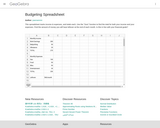
Tracking of income & expenses for student budgeting.
Water is a limited resource that we use over and over again. The idea is to teach the science behind the water cycle, where water comes from and is located on the Earth. After research and developing and understanding of conservation students will create a water tower that will collect and store rainwater. Students will also create a Public Service Announcement (PSA) on water conservation.
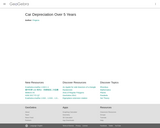
Car Depreciation Over 5 Years
On behalf of Marcus Caelius in the spring of 56 B.C.E. Roman oratory was a living art. Orators knew that the persuasive power of a speech did not come from the force and clarity of its argument alone. A speaker needed not simply to be heard distinctly, but to project the kind of confident, engaging personality that could win an audience's good will and command its belief.
Students participate in activities in which they learn about redistricting, types of legislative committees, types of legislation, and the process by which a bill becomes a law in Congress. Students will apply their knowledge by participating in a legislative simulation in which the House Judiciary Committee determines whether to report a proposed bill regarding punishment for drunk driving as favorable on the floor.