- Author:
- DAWNE COKER
- Subject:
- Mathematics
- Material Type:
- Activity/Lab, Lesson, Lesson Plan
- Level:
- Lower Primary
- Tags:
- License:
- Creative Commons Attribution
- Language:
- English
- Media Formats:
- Downloadable docs
Education Standards
T4T The Sandwich Problem

Overview
This resource is from Tools4NCTeachers.
In this lesson, students will determine ways to partition a sandwich into two equal parts and determine if the halves are the same size. Then students will work with partners to determine different ways to partition a sandwich into fourths and prove that the fourths are equal shares. Sample student work and recording sheets are provided within this lesson.
Remix this lesson to share extension activities and related math centers.
Here is a sample of this resource. Click the attachment to download the entire fully-formatted lesson and support materials.
The Sandwich Problem
During the mini lesson students will determine ways to partition a sandwich into two equal parts and determine if the halves are the same size. Then students will work with partners to determine different ways to partition a sandwich into fourths and prove that the fourths are equal shares. |
NC Mathematics Standard(s):
Geometry
NC.2.G.3 Partition circles and rectangles into two, three, or four equal shares.
- Describe the shares using the words halves, thirds, half of, a third of, fourths, fourth of, quarter of.
- Describe the whole as two halves, three thirds, four fourths.
- Explain that equal shares of identical wholes need not have the same shape.
Additional/Supporting Standards:
none
Standards for Mathematical Practice:
1. Make sense of problems and persevere in solving them.
3. Construct viable arguments and critique the reasoning of others.
4. Model with mathematics.
6. Attend to precision.
Student Outcomes:
- I can split a whole sandwich into halves.
- I can split a whole sandwich into fourths.
- I can use the terms half of, fourth of, or quarter of to describe parts of the sandwich.
- I can show that equal shares of a whole sandwich do not have to be the same shape or look the same.
Math Language:
What words or phrases do I expect students to talk about during this lesson?
Students will use the vocabulary from first and second grade such as: partition, half, half of, quarter of, fourth, whole, two halves, four fourths, rectangle, triangle.
Materials:
- 4” squares for mini lesson—6-8 squares—multiple colors of squares
- 4” squares—at least 6 per group—multiple colors of squares (The squares can be larger than 4” but all squares should be the same size.)
- Scissors for students
- Construction paper 12”x 24”—1 page per group
- Optional: geoboards and geobands, grid paper
Advance Preparation:
- Cut the squares before the class. It is helpful if the squares are a variety of colors.
Launch:
(The mini lesson could be done during one math class and the explore stage of the lesson could be done the next day.)
Mini Lesson: Determining Different Ways to Cut a Sandwich into Halves (15-20 minutes)
- Explain to your group that two children (you can choose two children from your class) have a sandwich. The bread is the same size. Show two of the 4” squares (Use two different colors for the squares.) and explain that these represent the sandwiches. Ask them to show you ways to cut the squares into two equal parts. Here are two possibilities:
- Possible questions to ask the group:
- What is the name for one part?
- How many halves are in the whole sandwich?
- How are the halves alike? Different?
- Explain to the class that the student with the rectangular halves thinks that the student with the triangular halves got larger halves.
- Show one of rectangle halves and one of the triangle halves and ask what they think.
- Have students explain their reasoning. Some students may want to cut one of the halves to show that they are equal. Have several squares available for students to cut and prove their thinking.
- Students may also work on geoboards to prove that the area of the triangle half is equal to the area of the rectangle half.
Explore:
Exploring Fourths of a Sandwich (30 minutes)
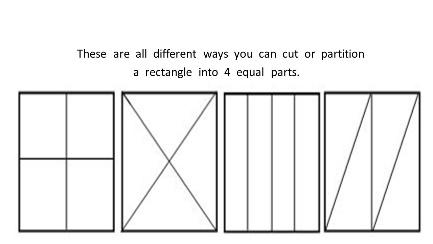
- Explain that four children all had sandwiches, but the sandwiches were cut differently. The sandwiches were all cut into four pieces but the children do not think that they each received the same amount. Show them these sandwiches cut into fourths.
- Questions to ask:
- How many parts are in each sandwich?
- What is each of those parts called?
- How are the fourths alike? Different?
- How does this problem relate to the ½ sandwich problem that we did earlier?
- Are the fourths the same size?
- They are going to work with a partner to determine if all the children received a fair share.
- Give them the paper squares you’ve cut and let them explore how to fold and cut the paper to make these fourths:
- Ask them to work with a partner to prove if the each child received a fair share. The partners will create a poster to prove their thinking. Explain that each poster should have a title, authors, their answer to the problem, and evidence of their answer.
- Some students may use grid paper or geoboards to prove their answer.
- Give each partnership 15-20 minutes to explore the problem and create their poster.
Discuss:
Discussion of the Sandwich Problem 15-20 minutes
1. After the partners have finished their posters decide how they will share their thinking. Each partnership could share to the whole class or two children could share with another partnership.
2. Possible questions to ask as children are sharing:
a.. Tell me how you started?
b. You seemed convinced that the fourths are the same (different) size, even though they are different shapes. How did you use the paper squares to prove your thinking?
c. How does knowing that all the sandwiches started as the same size help you?
d. How are the fourths alike? How are they different?
e. If you cut a sandwich into thirds would the pieces be the same, smaller or larger than the fourths. How do you know?
Evaluation of Student Understanding
Informal Evaluation: As the students are working in partnerships ask questions. Several possible questions are listed above. Record their responses. Take pictures of the posters as evidence of their work.
Formal Evaluation/Exit Ticket: the activity sheet
Meeting the Needs of the Range of Learners
Intervention:
Some children may not understand the Launch part of this lesson. They may need to work with halves of a square and prove that differently shaped halves are equal. After working with the squares have them work with longer rectangles and prove that differently shaped halves of the rectangles are equal.
Extension:
- Have students show two or three different ways to decompose a rectangle into fourths. Then have them prove that the fourths are equal.
- Have students work on geoboards to prove different shaped parts of a whole are equal in area.
- Have students divide a geoboard into fourths but each fourth is a different shape.
Possible Misconceptions/Suggestions:
|
|
Special Notes:
- As students cut their squares into halves or fourths they may not cut precisely. If their squares are imprecise, they may not be able to prove that the fractional pieces are equal.
- Students also may trim pieces to fit.
- If students are having trouble cutting precisely, the teacher may need to help them cut or students could use geoboards to prove the fractional parts are equal.
Possible Solutions:
This lesson is adapted from Bridges in Mathematics, Second Edition Teacher Guide, Second Grade, Unit 6. Published by The Math Learning Center, Salem, Oregon2013
Activity Sheet
Name ____________________________ Date ___________________
- Partition the rectangles in 2 different ways to show equal shares.
- 2 halves
|
|
Are the halves equal? Why or why not?
- 4 fourths
|
|
Are the fourths equal? Why or why not?