Read the Fine Print
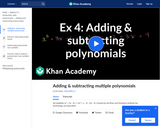
This video simplifies (x^3+ 3x - 6) + (-2x^2 + x - 2) - (3x - 4).
- Subject:
- Mathematics
- Material Type:
- Demonstration
- Provider:
- Khan Academy
- Date Added:
- 03/01/2018
Updating search results...
15 Results
Read the Fine Print
In this lesson, students use the distributive property to multiply a monomial by a polynomial and understand that factoring reverses the multiplication process. Students use polynomial expressions as side lengths of polygons and find area by multiplying. Students recognize patterns and formulate shortcuts for writing the expanded form of binomials whose expanded form is a perfect square or the difference of perfect squares.
- Subject:
- Mathematics
- Material Type:
- Lesson Plan
- Provider:
- EngageNY
- Date Added:
- 08/13/2018
Read the Fine Print
Using tiles to represent variables and constants, learn how to represent and solve algebra problem. Solve equations, substitute in variable expressions, and expand and factor. Flip tiles, remove zero pairs, copy and arrange, and make your way toward a better understanding of algebra.
- Subject:
- Math 1
- Math 2
- Math 3
- Mathematics
- Material Type:
- Interactive
- Provider:
- National Council of Teachers of Mathematics
- Author:
- Illuminations
- Date Added:
- 02/26/2019
Conditional Remix & Share Permitted
CC BY-NC
- Subject:
- Math 1
- Material Type:
- Lesson Plan
- Author:
- Rebecca Welch
- Date Added:
- 07/30/2019
Read the Fine Print
Worksheet on basic polynomial operations.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Kuta Software
- Date Added:
- 03/01/2018
Read the Fine Print
Find remainders, by using long division and the Remainder Theorem, to help decipher a message.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- MathBitsNotebook.com
- Date Added:
- 04/03/2018
Read the Fine Print
Students explore this interactive math tool and try to figure out what's happening on their own to discover the value of (a + b)^2?
- Subject:
- Math 1
- Math 2
- Mathematics
- Material Type:
- Activity/Lab
- Interactive
- Lesson Plan
- Provider:
- National Council of Teachers of Mathematics
- Author:
- Illuminations
- Date Added:
- 02/26/2019
Read the Fine Print
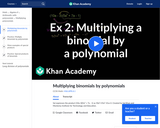
This video expresses the product (10a-3)(5a^2 + 7a - 1) as 50a^3+55a^2-31a+3.
- Subject:
- Mathematics
- Material Type:
- Demonstration
- Provider:
- Khan Academy
- Date Added:
- 03/01/2018
Read the Fine Print
Website that covers polynomial arithmetic with more than one variable.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Montemath
- Date Added:
- 02/20/2018
Read the Fine Print
Students will draw on their foundation of the analogies between polynomial arithmetic and base-ten computation, focusing on properties of operations, particularly the distributive property. Students identify and make connections between zeros of polynomials and solutions of polynomial equations.
- Subject:
- Math 1
- Math 2
- Math 3
- Mathematics
- Material Type:
- Unit of Study
- Provider:
- EngageNY
- Author:
- EngageNY
- Date Added:
- 02/26/2019
Read the Fine Print
Students will look at multiplying monomials, then monomials by
polynomials and finish with polynomials by polynomials.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Wallace Faculty
- Date Added:
- 02/27/2018
Read the Fine Print
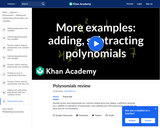
In this video, students quickly review what polynomials are, common related terms (e.g. degree, coefficient, binomial, etc.), addition & subtraction of polynomials, and modeling area with polynomials.
- Subject:
- Mathematics
- Material Type:
- Demonstration
- Provider:
- Khan Academy
- Date Added:
- 03/01/2018
Read the Fine Print
Practice worksheet on multiplying polynomials with solutions.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Wallace Faculty
- Date Added:
- 02/27/2018
Read the Fine Print
Students will analyze and explain precisely the process of solving an equation. Through repeated reasoning, students develop fluency in writing, interpreting, and translating between various forms of linear equations and inequalities and make conjectures about the form that a linear equation might take in a solution to a problem.
- Subject:
- Math 1
- Math 2
- Math 3
- Mathematics
- Material Type:
- Unit of Study
- Provider:
- EngageNY
- Author:
- EngageNY
- Date Added:
- 02/26/2019
Read the Fine Print
This video simplifies (4x^2y - 3xy + 25) - (9y^2x + 7xy - 20).
- Subject:
- Mathematics
- Material Type:
- Demonstration
- Provider:
- Khan Academy
- Date Added:
- 03/01/2018