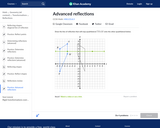
In this Khan Academy activity, students will find the line of reflection or draw the reflection of a shape over a given line.

CK-12 Foundation's Geometry FlexBook is a clear presentation of the essentials of geometry for the high school student. Topics include: Proof, Congruent Triangles, Quadrilaterals, Similarity, Perimeter & Area, Volume, and Transformations.

Students will study transformations and the role transformations play in defining congruence. The need for clear use of language is emphasized through vocabulary, the process of writing steps to perform constructions, and ultimately as part of the proof-writing process.

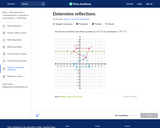
In this Khan Academy activity, students will find the line of reflection that reflects the given shape and it's reflection.

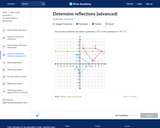
In this Khan Academy activity, students will find the line of reflection that reflects the given shape and it's reflection.

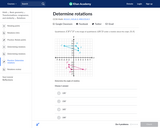
In this Khan Academy activity, students will find the angle of rotation of a given shape and it's image.

Students learn the relationship between a reflection and a rotation.
Students examine rotational symmetry within an individual figure.

This is a PBL project that asked students to select a select a major period/style of architecture in history, research it to see how this genre influenced the major architectural design elements, and then synthesize the information as part of a redesigned college campus. The final designs are presented to working architects and used as a basis to prove key geometry standards in the Math 2 curriculum.

Reference sheet for students and/or teachers that describes everything necessary to understand transformations and congruence and simalirity

This task allows students to extend their work with symmetries of quadrilaterals and practice making conjectures about geometric figures that are based on reasoning with the definitions of reflection and rotation. The work of this task will be revisited in Mathematics II, where students will be asked to create formal proofs for the conjectures they are making in this task about the properties of different types of quadrilaterals. Therefore, while this is classified as a practice understanding task, the mathematics students should be practicing is making and justifying conjectures about geometric figures based on the definitions of rigid-motion transformations, rather than practicing knowledge about the specific properties of different types of quadrilaterals. Whatever properties about sides, angles and diagonals of quadrilaterals students surface is sufficient for this task.

In this learning cycle, students focus on classes of geometric figures that can be carried onto themselves by a transformation—figures that possess a line of symmetry or rotational symmetry. In this task the idea of “symmetry” is surfaced relative to finding lines that reflect a figure onto itself, or determining if a figure has rotational symmetry by finding a center of rotation about which a figure can be rotated onto itself. This work is intended to be experimental (e.g., folding paper, using transparencies, using technology, measuring with ruler and protractor, etc.), with the definitions of reflection and rotation being called upon to support students’ claims that a figure possesses some type of symmetry. The particular classes of geometric figures considered in this task are various types of quadrilaterals.

In this task, students continue to focus on classes of geometric figures that can be carried onto themselves by a transformation—figures that possess a line of symmetry or rotational symmetry. Students solidify the idea of “symmetry” relative to finding lines that reflect a figure onto itself, or determining if a figure has rotational symmetry by finding a center of rotation about which a figure can be rotated onto itself. They also look for and describe the structure that determines if a figure possesses some type of symmetry. This work can be experimental (e.g., folding paper, using transparencies, using technology, measuring with ruler and protractor, etc.), or theoretical, with the definitions of reflection and rotation being called upon to support students’ claims that a figure possesses some type of symmetry.

The particular classes of geometric figures considered in this task are various types of regular polygons, and students will look for patterns in the types and numbers of lines of symmetry a regular polygon with an odd number of sides possesses, versus those with an even number of sides. They should also note a pattern between the smallest angle of rotation that carries a regular polygon onto itself and the number of sides of the polygon.

In this Khan Academy activity, students will answer questions about the symmetry of quadrilaterals, triangles, and regular polygons.

Informational text about reflections, image of reflected figure with hot spots, images of special reflections (x-axis, y-axis, x=y), interactive drag and drop reflected points of triangle.

Informative text followed by images with hot spots describing rotation of an object around a point.

Students will practice reflection/transltion of shapes with a card set and white boards. This is a lesson plan used to teach high school geometry. Materials are provided with the lesson.