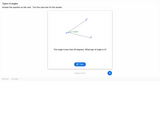
This is a ten question assessment afer a lesson taught on angle relationships and parallel lines.
In this task students are asked to develop a strategy for locating the center of a rotation, which leads to the observation that the center of rotation lies on the perpendicular bisectors of the segments joining image/pre-image pair of points. Such segments are defined to be chords of the circles on which the image/pre-image points are located. This work provides a method for finding the center of a circle. Students should also be able to prove that the perpendicular bisector of a chord contains a diameter of the circle and that the central angle formed by the radii that pass through the endpoints of the chord is bisected by the perpendicular diameter.
The purpose of this and the following task is to give students practice in analyzing diagrams to identify conjectures, and then writing proofs to show that the conjectures are true. The specific theorems being examined in this and the following task are:
• Vertical angles are congruent • The measure of an exterior angle of a triangle is the sum of the two remote interior angles
• When a transversal crosses parallel lines, alternate interior angles are congruent, corresponding angles are congruent, and same-side interior angles are supplementary (add to 180°).
Students will study transformations and the role transformations play in defining congruence. The need for clear use of language is emphasized through vocabulary, the process of writing steps to perform constructions, and ultimately as part of the proof-writing process.
The purpose of this task is to continue developing the ideas of formal proof, particularly moving from reasoning with a diagram to reasoning based on a logical sequence of statements that start with given assumptions and lead to a valid conclusion. Reasoning with a diagram is an important geometric thinking skill, and in this task students explore the logic behind the construction of diagrams—what features of a diagram must precede the addition of other features. Students also examine the diagram for possible conclusions that can be made—what else must be true. The last part of the task focuses on writing symbolic statements to match the verbal descriptions we are making about the diagram, and then to sequence those statements into a logical flow of ideas. The format of this work is suggestive of a two-column proof.
Explore flat geometry (Euclidean) that is based on figures on a plane versus spherical geometry (non-Euclidean) that is based on figures on a curved surface.
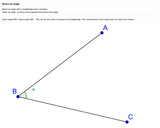
Images of construction of angle bisector, with descriptive text and hotspots of key points on images.
Images of construction of copying a line segment, with descriptive text and hotspots of key points on images.
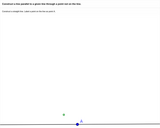
Images of construction of copying a line segment, with descriptive text and hotspots of key points on images.
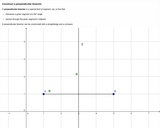
Images of construction of perpendicular bisector, with descriptive text and hotspots of key points on images.
This video explains how the properties of a perpendicular bisector are discovered.
11 dialog cards with images, each card contains an angle type, description, and definition of different types of angles.
The Teacher's Edition covers tips, common errors, enrichment, differentiated instruction and problem solving for teaching CK-12's Basic Geometry Student Edition. The solution and assessment guides are available upon request.
Dialog cards with image and definition of point, line, line segment, line, distance, angle, circle, parallel lines, perpendicular lines
Students apply the equilateral triangle construction to more challenging problems.
Students communicate mathematical concepts clearly and concisely.
Students write unknown angle proofs involving auxiliary lines.
Students write unknown angle proofs involving known facts.
Students review formerly learned geometry facts and practice citing the geometric justifications in anticipation of unknown angle proofs.
Students review formerly learned geometry facts and practice citing the geometric justifications in anticipation of unknown angle proofs.
Students review formerly learned geometry facts and practice citing the geometric justifications regarding angles in a triangle in anticipation of unknown angle proofs.