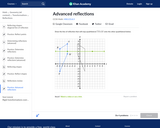
In this Khan Academy activity, students will find the line of reflection or draw the reflection of a shape over a given line.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Khan Academy
- Date Added:
- 08/17/2018

In this Khan Academy activity, students will find the line of reflection or draw the reflection of a shape over a given line.
CK-12 Foundation's Geometry FlexBook is a clear presentation of the essentials of geometry for the high school student. Topics include: Proof, Congruent Triangles, Quadrilaterals, Similarity, Perimeter & Area, Volume, and Transformations.

In Math 8 students came to understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations. In this task students are given two congruent figures and asked to describe a sequence of transformations that exhibits the congruence between them. While exploring potential sequences of transformations, students will notice how corresponding parts of congruent figures have to be carried onto one another, and they may look for ways that this can be accomplished in a consistent sequence of steps.

Students will understand transformations by first exploring the notion of linearity in an algebraic context. This quickly leads to a return to the study of complex numbers and a study of linear transformations in the complex plane.

Students will study transformations and the role transformations play in defining congruence. The need for clear use of language is emphasized through vocabulary, the process of writing steps to perform constructions, and ultimately as part of the proof-writing process.
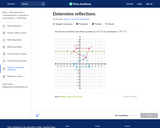
In this Khan Academy activity, students will find the line of reflection that reflects the given shape and it's reflection.
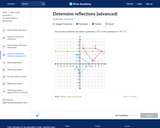
In this Khan Academy activity, students will find the line of reflection that reflects the given shape and it's reflection.
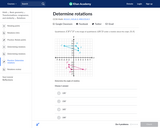
In this Khan Academy activity, students will find the angle of rotation of a given shape and it's image.
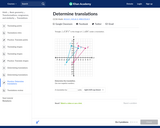
In this Khan Academy activity, students will determine the translation of a given shape.
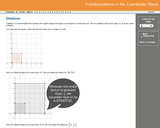
From Georgia Virtual school. Gret resource explaining dilations and scale factors
Students learn to construct a line parallel to a given line through a point not on that line using a rotation by 180˚. They learn how to prove the alternate interior angles theorem using the parallel postulate and the construction.
This video shows students how to graph translations.
In this Khan Academy activity, students will identify which transformation was performed between two images.

The purpose of this task is to continue solidifying the definitions of the rigid-motion transformations. Building on the work started in Leaping Lizards, students describe translations, rotations and reflections in terms of the important features that define these transformations, such as the distance from the center of rotation or from the line of reflection. Students will also surface the idea that it may take a combination of transformations to move from one image to another.

This task provides an opportunity for formative assessment of what students already know about the three rigid-motion transformations: translations, reflections, and rotations. As students engage in the task they should recognize a need for precise definitions of each of these transformations so that the final image under each transformation is a unique figure, rather than an ill-defined sketch. The exploration and subsequent discussion described below should allow students to begin to identify the essential elements in a precise definition of the rigid-motion transformations, e.g., translations move points a specified distance along parallel lines; rotations move points along a circular arc with a specified center and angle, and reflections move points across a specified line of reflection so that the line of reflection is the perpendicular bisector of each line segment connecting corresponding pre-image and image points.
In this Khan Academy activity, students will map a movable shapen to a given shape by using translations, rotations, and/or reflections.
In this Khan Academy activity, students will plot the image of a point under a reflection across a given line.
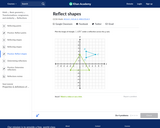
In this Khan Academy activity, students will plot the image of a shape under a reflection across a given line.
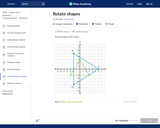
In this Khan Academy activity, students will plot the image of a shape that is rotated about the origin.
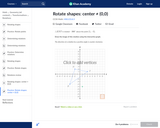
In this Khan Academy activity, students will plot the image of a shape that is rotated about a center that is not the origin.