Students are expected to learn how to factor polynomials with an emphasis on quadratic expressions.
Students develop the distributive property for application to polynomial multiplication. Students connect multiplication of polynomials with multiplication of multi-digit integers.
Students apply polynomial identities to the detection of prime numbers.
Students will factor certain forms of polynomial expressions by using the structure of the polynomials.
Students will use the structure of polynomials to identify factors.
Students will use the factored forms of polynomials to find zeros of a function.
Students will use the factored forms of polynomials to sketch the components of graphs between zeros.
Students graph polynomial functions and describe end behavior based upon the degree of the polynomial.
Students learn to fit polynomial functions to data values.
Students model a cross-section of a riverbed with a polynomial function and estimate fluid flow with their algebraic model.
The purpose of this task is to extend the Fundamental Theorem of Algebra from quadratic functions to cubic functions. The task asks students to use graphs and equations to find roots and factors and to consider the relationship between them. Students will also consider quadratic and cubic functions with multiple real roots and imaginary roots.
Students find a rule that agrees with a giventable. The mathematics task is intended to be a problem or question that encourages the use of mathematical practices. The dialogue is meant to show how students might engage in the mathematical practices as they work on the task.
Worksheet finding zeros of a polynomial and building polynomials given its zeros.
This article shows how to build general polynomials from their zeroes.
Students see how well they understand function expressions by trying to match the function graph to a generated graph. They may choose from several function types or select random and let the computer choose.
The purpose of this task is for students to find roots of polynomials and write the polynomials in factored form. This task builds on previous algebraic work, including factoring, polynomial long division, and quadratic formula. Students also use their knowledge of the Fundamental Theorem of Algebra to know how many roots a function has and to consider the possible combinations of real and imaginary roots for polynomials of degree 1-4. Students learn that imaginary roots occur in conjugate pairs and use this knowledge to both find roots and know the possible combinations of roots for polynomials.
Notes that help students chose the method for solving a polynomial.
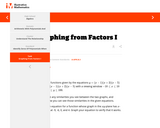
The purpose of this task is to help students understand the relationship between the factors of a polynomial and the x-intercepts of the graph of the polynomial.
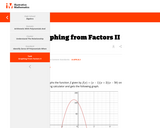
The purpose of this task is to give students an opportunity to see and use the structure of the factored form of a polynomial. The factor x−50 tells them that they should include x=50 in the range on the x-axis. Students might also draw on their knowledge of the long run behavior of a cubic polynomial to recognize that Emery's graph must eventually return across the x-axis to the right of his current viewing window.
The task has students use the remainder theorem to deduce a linear factor of a cubic polynomial, and then to completely factor the polynomial. Students will need some procedure (e.g., synthetic or long division, or guess-and-check the coefficients) for determining the quadratic factor. Having the factored form permits students to deduce much about the structure of the graph.
Worksheet on factoring and finding zeros of a polynomial and building polynomials given its zeros.