- Author:
- DAWNE COKER
- Subject:
- Mathematics
- Material Type:
- Activity/Lab, Lesson, Lesson Plan
- Level:
- Lower Primary
- Tags:
- License:
- Creative Commons Attribution
- Language:
- English
- Media Formats:
- Downloadable docs
Education Standards
arrow-cards-to-1000-nbt3
T4T Arrow Cards
Overview
This resource is from Tools4NCTeachers.
In this lesson, students develop an understanding of place value by using arrow cards. The focus of this lesson is on writing numbers using expanded form.
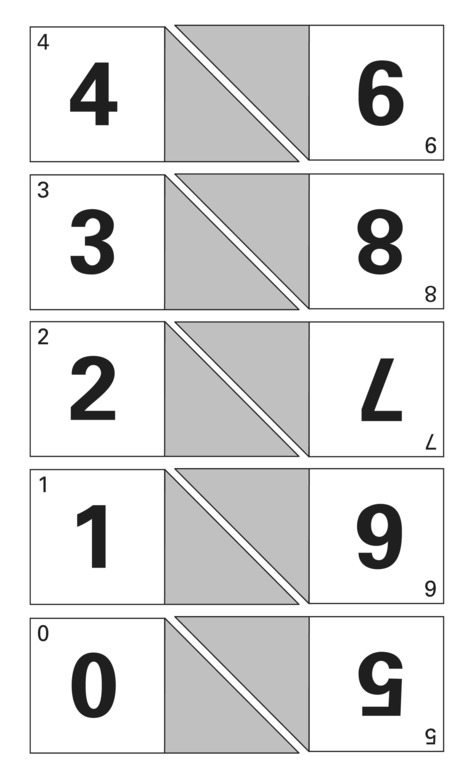
Arrow cards are place value cards with an "arrow" or point on the right side. Students can organize the cards to represent numbers in expanded notation. OR, they can overlap cards and (lining up the arrows) to form multi-digit numbers. Printable arrow cards are provided with this resource..
This is a sample from the lesson. Click the attachment to view the entire, fully-formatted lesson and support materials.
In this lesson, students develop an understanding of place value by using arrow cards. It explores how numbers can be written using expanded form. |
Arrow Cards to 1000
Common Core Standard:
Understand place value.
NC.2.NBT.3 Read and write numbers to 1000 using base-ten numerals, number names, and expanded form.
Additional/Supporting Standard:
Understand place value.
NC.2.NBT.1 Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., 706 equals 7 hundreds, 0 tens, and 6 ones. Understand the following as special cases:
- 100 can be thought of as a bundle of ten tens – called a “hundred.”
- The numbers 100, 200, 300, 400, 500, 600, 700, 800, 900 refer to one, two, three, four, five, six, seven, eight, or nine hundreds (and 0 tens and 0 ones).
Standards for Mathematical Practice:
1. Make sense of problems and persevere in solving them.
2. Reason abstractly and quantitatively.
4. Model with mathematics.
6. Attend to precision.
Student Outcomes:
- I can read and write numbers up to 1000 using base-ten numerals.
- I can read and write numbers using expanded form.
- I can represent each digit in a three-digit number.
Materials:
- Arrow Cards
- Math journals or paper
Advance Preparation:
- Arrow cards will be copied, cut and stored in bags prior to beginning this task.
- Some students will have used arrow cards in previous grades and know how to line up the arrows. If students have not used arrow cards before the teacher will need to allow time for exploration of the cards.
Directions:
- If students have not used arrow cards before demonstrate that the arrows must always be on top of each other when you are making a number. Students sort cards into groups of ones, tens, and hundreds. Students will be working with a partner.
- After the students have sorted the cards the teacher begins by asking students in their pairs to show numbers such as 3, 6, 7, show me 50, 80, 30, show me 200,600,900.The teacher will also write the number on the board. When they show the number the teacher can say “how many tens in 20 to reinforce the idea of 20 as 2 tens. Some students may still be trying to place a 5 next to a 52 to build 52. If this happens remind students that the arrows need to go on top of each other when numbers are being built.
- The teacher needs to encourage students to share their connections and observations as the students are building numbers. For example, some students will notice that building the numbers is the same as adding the numbers. The idea of expanded form can then be taught using written notation showing the addition of each number as in 137= 100 + 30 + 7.
- The teacher will want students to show 2 numbers such as 15 and 51” One student can build one number and the other student in the pair can build the other. Both numbers should be placed in front of the students so they can discuss the difference between the value of the 5 in 15 and the 5 in 51. Again, the ‘one’ digit can be removed to reveal the value of the 5 in 51.
- Students need to have examples of 0 in the middle of the number use numbers such as 500, 309, and 120.
- Students can now provide the numbers for the class to build asking each pair to build them and to write each number they built in expanded form and standard form in their journals or on a piece of paper.
Questions to Pose:
Before:
Show the arrow cards and asks students to show you how we build numbers with them?
During:
Ask students to demonstrate different numbers, such as 51, 15, 500, and 309.
How many tens/ hundreds are in your number?
Show me how to write this number in expanded form.
After:
How do arrow cards help us with expanded form?
How do arrow cards help us with writing numbers in standard form?
Possible Misconceptions/Suggestions:
Possible misconceptions | Suggestions |
Students may be challenged by writing numbers that they read or hear and think that 285 is 200805. | Use of the arrow cards to help students understand the value of each place and then how to write that number. |
Special Notes:
Some students will have used arrow cards in previous grades and know how to line up the arrows. If students have not used arrow cards before the teacher will need to allow time for exploration of the cards. This task is to be completed prior to the task on 2.NBT.5.
Solutions: NA
Adapted from Partners for Mathematics Learning 2009
This is a sample from the lesson. Click the attachment to view the entire, fully-formatted lesson and support materials.
In this lesson, students develop an understanding of place value by using arrow cards. It explores how numbers can be written using expanded form. |
Arrow Cards to 1000
Common Core Standard:
Understand place value.
NC.2.NBT.3 Read and write numbers to 1000 using base-ten numerals, number names, and expanded form.
Additional/Supporting Standard:
Understand place value.
NC.2.NBT.1 Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., 706 equals 7 hundreds, 0 tens, and 6 ones. Understand the following as special cases:
- 100 can be thought of as a bundle of ten tens – called a “hundred.”
- The numbers 100, 200, 300, 400, 500, 600, 700, 800, 900 refer to one, two, three, four, five, six, seven, eight, or nine hundreds (and 0 tens and 0 ones).
Standards for Mathematical Practice:
1. Make sense of problems and persevere in solving them.
2. Reason abstractly and quantitatively.
4. Model with mathematics.
6. Attend to precision.
Student Outcomes:
- I can read and write numbers up to 1000 using base-ten numerals.
- I can read and write numbers using expanded form.
- I can represent each digit in a three-digit number.
Materials:
- Arrow Cards
- Math journals or paper
Advance Preparation:
- Arrow cards will be copied, cut and stored in bags prior to beginning this task.
- Some students will have used arrow cards in previous grades and know how to line up the arrows. If students have not used arrow cards before the teacher will need to allow time for exploration of the cards.
Directions:
- If students have not used arrow cards before demonstrate that the arrows must always be on top of each other when you are making a number. Students sort cards into groups of ones, tens, and hundreds. Students will be working with a partner.
- After the students have sorted the cards the teacher begins by asking students in their pairs to show numbers such as 3, 6, 7, show me 50, 80, 30, show me 200,600,900.The teacher will also write the number on the board. When they show the number the teacher can say “how many tens in 20 to reinforce the idea of 20 as 2 tens. Some students may still be trying to place a 5 next to a 52 to build 52. If this happens remind students that the arrows need to go on top of each other when numbers are being built.
- The teacher needs to encourage students to share their connections and observations as the students are building numbers. For example, some students will notice that building the numbers is the same as adding the numbers. The idea of expanded form can then be taught using written notation showing the addition of each number as in 137= 100 + 30 + 7.
- The teacher will want students to show 2 numbers such as 15 and 51” One student can build one number and the other student in the pair can build the other. Both numbers should be placed in front of the students so they can discuss the difference between the value of the 5 in 15 and the 5 in 51. Again, the ‘one’ digit can be removed to reveal the value of the 5 in 51.
- Students need to have examples of 0 in the middle of the number use numbers such as 500, 309, and 120.
- Students can now provide the numbers for the class to build asking each pair to build them and to write each number they built in expanded form and standard form in their journals or on a piece of paper.
Questions to Pose:
Before:
Show the arrow cards and asks students to show you how we build numbers with them?
During:
Ask students to demonstrate different numbers, such as 51, 15, 500, and 309.
How many tens/ hundreds are in your number?
Show me how to write this number in expanded form.
After:
How do arrow cards help us with expanded form?
How do arrow cards help us with writing numbers in standard form?
Possible Misconceptions/Suggestions:
Possible misconceptions | Suggestions |
Students may be challenged by writing numbers that they read or hear and think that 285 is 200805. | Use of the arrow cards to help students understand the value of each place and then how to write that number. |
Special Notes:
Some students will have used arrow cards in previous grades and know how to line up the arrows. If students have not used arrow cards before the teacher will need to allow time for exploration of the cards. This task is to be completed prior to the task on 2.NBT.5.
Solutions: NA
Adapted from Partners for Mathematics Learning 2009